File Excel su OneDrive
colletti-giovanni@virgilio.it

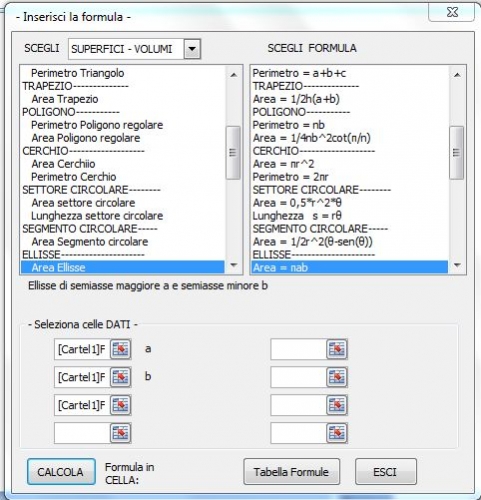
Con il tasto formule compare la finestra a fianco.
Cliccando in uno dei 2 box si può selezionare una formula, ad esempio: Area ellisse .
Nel box di sinistra sono inserite le descrizioni “Area ellisse” in quello di destra sono inserite le formule “Area=π*a*b”.
Sotto viene riportata la descrizione “Ellisse di semiasse maggiore a e semiasse minore b”.
Seleziona le celle dati in cui, in precedenza, erano stati inseriti i valori di a e b.
Con calcola la formula viene scritta nella cella indicata e che era selezionata prima di scegliere la formula.
Questo programma permette di creare una libreria di formule personali.
La costruzione di tali funzioni avviene direttamente in Excel.
Come caricare il file
– Scaricare con Salva il file “Formulario.xla”, dandogli il nome “Formulario.xla” e salvarlo in una cartella;
– Scaricare con Salva il file Formulario1.xls, dandogli il nome “Formulario1.xls” e salvarlo nella cartella “C:\Users\Public\” cioè “C:\Utenti\Pubblica” ;
– Aprire un qualsiasi file Excel, selezionare dal menù Strumenti la voce “Componenti Aggiuntivi”. Nella finestra che appare premere il pulsante Sfoglia e cercare il file aggiuntivo Formulario e caricarlo (ovviamente lo cercheremo nella cartella dove l’avremo precedentemente salvato). Una volta acquisito il file, nella finestra “Componenti aggiuntivi disponibili“, vedremo comparire il componente aggiuntivo Formulario;
– Nel nostro file excel sarà visualizzata un nuova barra strumenti con il tasto Formula, con esse è possibile utilizzare le formule.
Potremo, a nostro piacere, aggiungere tutte le funzioni che desideriamo, in modo da creare un proprio archivio di formule disponibile ogni volta che apriremo in Excel.
Per approfondire leggi il file Guida_formulario.doc.
 dal sito di www.lescienze.it del 11/10/2012
dal sito di www.lescienze.it del 11/10/2012
Una muffa unicellulare, Physarum polycephalum, detta anche melma policefala, è in grado esplorare un labirinto senza ritornare sui percorsi già battuti, dove evidentemente “ricorda” di essere già passata, poiché, pur essendo priva di un sistema nervoso, sfrutta come “memoria esterna” una sua secrezione. La scoperta arriva da una ricerca ispirata allo studio dei movimenti dei robot mobili autonomi.
Gli automi cellulari riescono ad imitare il comportamento di questa muffa!!!
Ma che cosa è un automa cellulare? Consiste di una griglia costituita da celle, per ogni cella è necessario definire l’insieme delle celle che sono da considerare “vicine” alla cella data. Ogni cella cambierà valore contemporaneamente a tutte le altre, secondo una regola fissata che è funzione delle celle vicine. Nel post Il labirinto e gli automi cellulari l’automa cellulare Celle Autome2.xls trova il percorso di uscita del labirinto.

Ad esempio. Fissato il valore iniziale 1 o 0 delle celle, inseriamo in ogni cella la condizione: se la somma delle celle confinanti è minore o uguale a 1 la cella assume valore 0; se la somma, invece, è maggiore di 1 la cella assume valore 1. Ad ogni step tutte le celle della griglia vengono ricalcolate, tenendo conto delle celle confinanti.

Dopo varie iterazioni vengono colorate di bianco tutte le celle che appartengono ai rami a fondo cieco (rami secchi), mentre rimangono in rosso solo le celle che formano il percorso ed eventuali percorsi chiusi. Si nota, nella figura seguente, che le celle bianche appartengono ai rami con il fondo cieco e non fanno parte del percorso.

Il Gioco della vita: Il gioco della vita è costituita da un’infinita griglia bidimensionale di celle quadrate, ognuna delle quali si può trovare in due possibili stati, vivo o morto. Ogni cella può interagire con le sue otto celle adiacenti. Ad ogni step temporale le celle vengono aggiornate secondo le seguenti regole: 1. Ogni cella viva con meno di due vicini vivi muore, a causa di isolamento; 2. Ogni cella viva con due o tre vicini vivi sopravvive; 3. Ogni cella viva con più di tre vicini vivi muore, a causa di sovrappopolazione; 4. Ogni cella morta con esattamente tre vicini vivi diventa una cella viva. Il motivo per cui questo automa ha attratto grande interesse è a causa del sorprendente modo con cui i pattern di celle possono evolvere. Nel gioco della vita si possono osservare esempi di auto-organizzazione e la nascita di comportamenti emergenti.
LA MEMORIA DELL’ACQUA
 Nel regno animale, l’acqua rappresenta una quota compresa tra il 90-95% negli organismi inferiori e il 70-80% in quelli superiori, uomo in testa. E all’interno delle strutture biologiche, l’acqua si può trovare sia come una molecola sia in forma combinata. In realtà, l’acqua ha ancora molti «segreti», potendo per esempio agire come fattore di risonanza magnetica all’interno delle cellule e riuscire a modificare la sua concentrazione in funzione dell’invecchiamento. Si può dire che siamo fatti d’acqua: il corpo di un bambino è composto di liquidi per l’80%, quello di un adulto per il 60%. Solo negli anziani la percentuale scende un pochino (45%). E il cervello è l’organo che ne ha di più (85%): nelle cellule, tra le cellule, tutt’intorno. Galleggia. Così come nel grembo materno, il feto galleggia nel liquido amniotico.
Nel regno animale, l’acqua rappresenta una quota compresa tra il 90-95% negli organismi inferiori e il 70-80% in quelli superiori, uomo in testa. E all’interno delle strutture biologiche, l’acqua si può trovare sia come una molecola sia in forma combinata. In realtà, l’acqua ha ancora molti «segreti», potendo per esempio agire come fattore di risonanza magnetica all’interno delle cellule e riuscire a modificare la sua concentrazione in funzione dell’invecchiamento. Si può dire che siamo fatti d’acqua: il corpo di un bambino è composto di liquidi per l’80%, quello di un adulto per il 60%. Solo negli anziani la percentuale scende un pochino (45%). E il cervello è l’organo che ne ha di più (85%): nelle cellule, tra le cellule, tutt’intorno. Galleggia. Così come nel grembo materno, il feto galleggia nel liquido amniotico.
L’acqua ha una memoria? L’elemento che è all’origine della vita possiede anche una vita propria? La squadra di Voyager indaga sul funzionamento del nostro DNA e sul modo in cui i nostri geni possono trasmettere informazioni proprio attraverso l’acqua. A Parigi, Roberto Giacobbo incontra in esclusiva il premio nobel per la medicina Luc Montagnier, un grande scienziato che sta portando avanti una ricerca unica nel suo genere, una ricerca che potrebbe stravolgere molti dei principi della chimica e della biologia moderne.L’ipotesi di Montagnier, infatti, è che il nostro DNA possa trasmettersi a distanza attraverso onde elettromagnetiche che si diffondono nell’acqua. Un’idea che ha generato un vero e proprio terremoto nella comunità scientifica, proprio per l’autorevolezza di chi l’ha proposta.Voyager ha raccolto e messo a confronto il parere anche di altri studiosi, tra cui due illustri fisici italiani (Emilio Del Giudice e Giuseppe Vitiello), per capire i fondamenti che sono alla base di questa ricerca e quale potrebbero essere le conseguenza, a livello pratico e teorico, di una tale scoperta.
Ovvero, la molecola d’acqua «registra» le onde a bassa frequenza del Dna, le «memorizza» e le trasmette in un certo senso «amplificandole».
Il Dna è in grado di emettere e di trasmettere segnali elettromagnetici di bassa frequenza in soluzioni acquose altamente diluite, le quali mantengono poi «memoria» delle caratteristiche del Dna stesso.
Dal punto di vista chimico, la diluizione è talmente alta che alla fine del processo non rimane nessuna molecola. Da un certo punto in avanti, non si fa altro che diluire acqua con acqua. Per dare un’idea delle proporzioni una diluizione tra le meno estreme equivale a una goccia nell’Oceano Atlantico: un paradosso che sarebbe però spiegato dall’ipotesi della memoria dell’acqua, secondo la quale l’acqua sarebbe in grado di conservare il ricordo delle sostanze da cui è attraversata.
Insomma, il Dna «comunica» all’acqua che memorizza e divulga il messaggio.
vedi anche:
Documentario russo sui misteri dell’acqua
Traduzione dal russo all’italiano di Leandro e Ola
Ernst Chladni notò che il suono influisce sulla materia fisica ed ha la prerogativa di creare schemi geometrici.
Hans Jenny notò che quando venivano pronunciate le vocali delle antiche lingue fenicio-ebraica e sanscrita, la sabbia assumeva la forma dei simboli grafici delle vocali stesse mentre, d’altro canto, le nostre lingue moderne non producevano un analogo risultato !
Come è possibile ? Gli antichi Ebrei e gli Indiani ne erano a conoscenza ?
“Tutto l’universo è un insieme di risonanze armoniche derivanti da un unico suono, un vero e proprio ologramma che si conforma secondo i rapporti delle sue sovrarmoniche o sottoarmoniche, ovvero il rapporto tra le energie sottili e le vibrazioni lente”. (SANGLODEA, 2006).
John Keely: “La forza è la materia liberata, mentre la materia non è nient’altro che la forza cristallizzata”. Göthe: “La Musica è architettura svolta, mentre l’architettura è musica pietrificata”. Leonardo Da Vinci: “A le stesse leggi obbediscono le onde sia de l’acqua sia del suono e della luce”.
Questo capitolo ha lo scopo di familiarizzare con la teoria dei sistemi dinamici, facendo quasi del tutto a meno dell’apparato matematico.
L’uso della simulazione numerica al calcolatore, sempre più importante nello studio dei sistemi dinamici, costituisce parte integrante di questo processo. Oltre ad allenare fin da subito a mettere le mani sul calcolo scientifico, con tali processi formativi si mira a far nascere, in modo quasi spontaneo, concetti matematici profondi e sottili e vederli all’opera nel concreto, ovvero abituarsi a lavorare con la matematica per analizzare quantitativamente i fenomeni della natura.
I sistemi dinamici discreti, sono delle successioni per ricorrenza e costituiscono un settore della matematica molto vasto e con aspetti sorprendenti.
Nelle 3 immagini sono rappresentati 3 sistemi dinamici realizzati con formule relativamente semplici.

Esempi di sistemi dinamici discreti sono:
Concetti basilari comuni a tutti i sistemi dinamici sono i seguenti:
Continua a leggere con SDD Frattali , SDD Impedovo , SDD Wiki .
Calcola i SDD.xls
Crea il Triangolo e i poligoni di Sierpinski con Sierpinski.xls
Crea la Mappa_Logistica.xls
Crea i frattali di Mandelbrot e di Julia con Frattali.xls
Clicca sull’icona per aprire il programma.
Definita la figura piana di equazione y=f(t), viene calcolata: l’Area, i Momenti_Statici Sx e Sy, i Momenti d’Inerzia Mx e My e il Baricentro (xg;yg). Programma simile.
Clicca sull’icona per aprire la calcolatrice per numeri complessi.
I numeri complessi sono un’estensione dei numeri reali nata inizialmente per consentire di trovare tutte le soluzioni delle equazioni polinomiali. Ad esempio, l’equazione non ha soluzioni reali, perché in questo insieme non esistono numeri il cui quadrato sia negativo.Si definisce allora il valore i, chiamato anche unità immaginaria, che gode della seguente proprietà: e dunque: I numeri complessi sono formati da due parti, una parte reale ed una parte immaginaria, e sono rappresentati dalla seguente espressione: dove a e b sono numeri reali, mentre i è l’unità immaginaria.
Il perdono è il più grande dono di Dio dopo la vita. Ma dobbiamo eliminare ogni diffidenza per poterlo chiedere ed accogliere con gioia. E’ assolutamente necessaria la nostra sincera collaborazione.