Premessa. In ambito quantistico i fisici parlano di un mondo fatto di particelle e campi di forze, ma non è chiaro che cosa si intende per particelle e campi di forze, a riguardo si riporta l’articolo: Che cosa è reale? di Meinard Kuhlmann. Il problema dell’interpretazione quantistica inizia già con le domande i quanti h e gli elettroni sono onde o particelle?
Onde di Materia. Ad esempio nell’effetto Compton, che descrive l’urto perfettamente elastico tra un fotone e un elettrone, si ha la conservazione dell’energia e della quantità di moto del sistema fotone-elettrone. Da esso si ricava: La lunghezza d’onda di Compton λ = h/mv di una particella di energia E = m*c2 è uguale alla lunghezza d’onda di un fotone di uguale energia E = h*v. Cioè particelle e fotoni aventi uguali energie (m*c2 = h*v) hanno la stessa lunghezza d’onda (di Compton) λ.
Il Vuoto come campo quantizzato. Riprendiamo la relazione E = h*ν (1) scritta nella forma h = E/v si evince che il quanto h costituisce l’energia di una singola oscillazione (del campo elettrico e magnetico). Poiché il fotone h (onda elettromagnetica) si propaga nel vuoto solo per quanti h, si può supporre che il quanto h sia una proprietà del vuoto, ossia che il vuoto possa oscillare solo per quanti h = ΔE*Δt (con Δt tempo di una oscillazione). Valori di energia*tempo inferiori ad h non producono oscillazioni/perturbazione del vuoto. In breve, con queste poche considerazioni si è passati dalle particelle che hanno una lunghezza d’onda ai quanti che si possono ipotizzare delle perturbazioni del vuoto.
Rappresentazioni del quanto. Il quanto h ha le dimensioni dell’azione A cioè: massa*velocità*spazio e vale h= 6*10-34Js, per cui potrebbe essere costituito da una 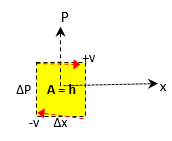 particella di massa m=E/c2 che si muove avanti e indietro con velocità +v e -v all’interno di una scatola di lunghezza Δx. Posta la variazione di velocità Δv = 2v, si ha: h= mΔv*Δx. Nel diagramma (mv ; x) detto spazio delle fasi, il quanto h è rappresentato dall’area m*2v*Δx. Se la particella è il fotone h con lunghezza d’onda λ = c/ν e velocità v= c (velocità della luce), quando il fotone/onda colpisce la parete l’onda riflessa interferisce con l’onda incidente, per cui: Se la lunghezza Δx della scatola è pari ad un numero interno di oscillazioni di lunghezza λ si ha una interferenza costruttiva fra l’onda incidente e l’onda riflessa; viceversa si ha una interferenza distruttiva delle due onde. Nel primo caso le onde incidenti e le onde riflesse creano le onde stazionarie, per cui il fotone (quanto) oscillando su tutta la lunghezza della scatola non può essere individuato in un punto, né ha una velocità in quanto onda stazionaria.
particella di massa m=E/c2 che si muove avanti e indietro con velocità +v e -v all’interno di una scatola di lunghezza Δx. Posta la variazione di velocità Δv = 2v, si ha: h= mΔv*Δx. Nel diagramma (mv ; x) detto spazio delle fasi, il quanto h è rappresentato dall’area m*2v*Δx. Se la particella è il fotone h con lunghezza d’onda λ = c/ν e velocità v= c (velocità della luce), quando il fotone/onda colpisce la parete l’onda riflessa interferisce con l’onda incidente, per cui: Se la lunghezza Δx della scatola è pari ad un numero interno di oscillazioni di lunghezza λ si ha una interferenza costruttiva fra l’onda incidente e l’onda riflessa; viceversa si ha una interferenza distruttiva delle due onde. Nel primo caso le onde incidenti e le onde riflesse creano le onde stazionarie, per cui il fotone (quanto) oscillando su tutta la lunghezza della scatola non può essere individuato in un punto, né ha una velocità in quanto onda stazionaria.
Il quanto h potrebbe essere costituito da una particella di massa/energia m= h/(c*λ) in rotazione attorno ad un punto distante r cioè dal vettore momento angolare o momento della quantità di moto: h = L = r /\ mv = r*P* sen(θ) (prodotto vettore) avente valore pari all’area del parallelogramma definito dai vettori r (distanza) e P (quantità di moto) e con direzione ortogonale al piano definito da tali vettori. Il prodotto vettore potrebbe essere calcolato anche come: Lz = rx *Py – ry*Px , da tale formula si nota che il prodotto vettore è anti-commutativo. Il quanto potrebbe, altresì, essere costituito da una particella con momento d’inerzia I in rotazione attorno al suo asse con velocità angolare ω: h = L = I*ω . Il fotone-quanto h è comunque un vettore costante costituito dal prodotto di due grandezze fisiche.
Quanti e orbitali Consideriamo un oscillatore armonico costituito da una particella fissata alla estremità di una molla in oscillazione, esso ha energia cinetica Ec = P2/2*m ed energia potenziale Ep = ½*k*x2. Poiché l’energia totale E deve essere costante si scrive: P2/2*m + ½*k*x2 = E → P2/2E*m + k/2E*x2 = 1.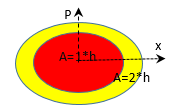 Questa è l’equazione dell’ellisse di semiassi a = √(2E*m) e b = √(2E/k) nello spazio delle fasi (P;x). Ricordiamo che l’area dell’ellisse è un’azione e vale: A = π*a*b =π*√(4E2*m/k) = 2π*E*√(m/k) = E*2π /ω = E*t. L’area dell’ellisse non può variare per valori infinitesimi ma solo per valori discreti: A= 1h, A= 2h, … Poiché l’azione A è quantizzata l’orbita di un elettrone, che ruota intorno a un nucleo atomico, viene interpretata come un’onda con una determinata lunghezza. Essa è quantizzata in quanto contiene un numero intero di quanti h. Cioè il momento angolare L della particella deve essere uguale ad un numero intero n di quanti h: L = m*v*r =n*h.
Questa è l’equazione dell’ellisse di semiassi a = √(2E*m) e b = √(2E/k) nello spazio delle fasi (P;x). Ricordiamo che l’area dell’ellisse è un’azione e vale: A = π*a*b =π*√(4E2*m/k) = 2π*E*√(m/k) = E*2π /ω = E*t. L’area dell’ellisse non può variare per valori infinitesimi ma solo per valori discreti: A= 1h, A= 2h, … Poiché l’azione A è quantizzata l’orbita di un elettrone, che ruota intorno a un nucleo atomico, viene interpretata come un’onda con una determinata lunghezza. Essa è quantizzata in quanto contiene un numero intero di quanti h. Cioè il momento angolare L della particella deve essere uguale ad un numero intero n di quanti h: L = m*v*r =n*h.
L’orbita dell’elettrone, come detto sopra contiene un numero intero di quanti h ossia di onde, per cui essa si comporta come una corda fissa agli estremi, di lunghezza l uguale a quella dell’orbita. Nella corda può sussistere solo un numero intero di onde di lunghezze l, l/2, l/3, … . Tali onde sono le onde stazionarie. Cioè l’orbita percorsa dall’elettrone è costituita da onde stazionarie nello spazio, ossia l’elettrone si muove all’interno di onde stazionarie. Vediamo di interpretare la relazione: m*v*r = n*h . Da essa si deduce che la particella m ruota con un momento della quantità di moto pari ad un numero intero n di oscillazioni h. Dal punto di vista energetico si può supporre che l’energia della particella E = 1/2*m*v2 venga utilizzata per perturbare il vuoto con un numero intero di oscillazioni E= h*v, ossia che la sua energia venga a distribuirsi nel vuoto come quanti h di perturbazione. Il vuoto viene quindi ad essere un campo di oscillazioni (energia E= h/Δt) quantizzato.
La materia come onde stazionarie. L’onda stazionaria è composta da due onde della stessa lunghezza e intensità ma con velocità v opposte ossia: v e –v. Le onde stazionarie hanno particolari proprietà:
- Non trasportano energia (l’onda ha velocita risultante nulla ma ampiezza doppia);
- Sono stabili (interferiscono costruttivamente fra loro);
- La sovrapposizione di più onde stazionarie è ancora un’onda stazionaria;
- Hanno quantità di moto nulla (essendo costituite da onde con velocità opposte);
- Accumulano energia ‘statica’ (l’energia è ferma ed è distribuita uniformemente su tutta l’onda).
Tutte queste proprietà ci inducono ad ipotizzare che la materia possa essere costituita da onde stazionarie. L’onda stazionaria, a differenza dell’onda singola, ha velocità nulla ed oscilla su tutto il suo sviluppo, tra massimo e minimo simultaneamente (i nodi dell’onda stazionaria rimangono fermi), essa inoltre non dipende dal tempo.
Orbita stazionaria dell’elettrone. Nel caso dell’orbita stazionaria dell’elettrone che ruota intorno al nucleo il pacchetto d’onda stazionario è descritto dalla funzione d’onda di Schrodinger Ψ. Un’onda stazionaria nella sola direzione x è definita dall’equazione differenziale: d2Ψ/d2x + 4π/λ2*Ψ = 0 in cui Ψ è la funzione d’onda e rappresenta l’ampiezza mentre λ la lunghezza d’onda.
Dalla relazione di De Broglie, che ipotizzò un comportamento ondulatorio anche per la materia, λ = h/mv sostituendo nell’equazione si ricava: d2Ψ/d2x + 4π h2/m2v2*Ψ = 0 inoltre poiché l’energia cinetica T è la differenza dell’energia totale E e dell’energia potenziale V, cioè: T = ½ m2v2 = E – V → d2Ψ/d2x + 8π h2/(E-V)*Ψ = 0 essa è la funzione d’onda stazionaria lungo x dell’elettrone.
L’intreccio quantistico Se consideriamo i due elettroni di uno stesso orbitale, per il principio di esclusione (di Pauli) essi hanno spin opposti ossia ruotano in senso opposto. I due elettroni inoltre risultano intrecciati (interconnessi) ossia: se si agisce su uno anche l’altro ne risente simultaneamente. Ritengo che la simultaneità di interazione tra le due particelle sia dovuta alla stazionarietà dell’orbitale, ossia che l’intreccio quantistico sia dovuto alla stazionarietà dell’onda a cui appartengono entrambi gli elettroni. I due elettroni intrecciati possono essere raffigurati come pacchetti d’onde aventi onde in comune.
Rappresentazione della particella come pacchetto d’onde stazionarie. Abbiamo visto che l’elettrone, come il fotone dentro la scatola, percorre orbite stazionarie con un numero intero n di onde o quanti h (ricordiamo la L = m*v*r =n*h). Consideriamo allora l’equazione di un’onda di lunghezza λ in moto con velocità v: A = sen(x/λ+ v*t/λ) (1). Osserviamo che la frequenza dell’onda: ν = (x/λ+ v*t/λ) = 1/λ*(x+ v*t) possiamo scomporla in una frequenza “spaziale”: νs= x e in una frequenza “temporale”: νt= v*t dovuta al moto e che, inoltre, lo spazio x e la velocità v sono simmetrici. E’ possibile allora avere onde in moto con x (lunghezze d’onda) e v (velocità) diverse ma stessa frequenza v. Ad esempio le onde con: (x= 1, v= 2), (x= 2, v= 1), (x= 2,5, v= 0,5) in un intervallo t= 1 hanno tutte frequenza v = 3/λ. Esse cioè hanno nel tempo t quanti h uguali: h/Δt = cost cioè stessa energia h*ν = E = cost. L’insieme di tali onde di lunghezze diverse possono formare allora un pacchetto d’onde più o meno compatto: Ossia 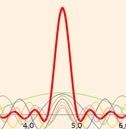 più le lunghezza d’onda λi (velocità vi) sono diverse (Δv grande) più il pacchetto è concentrato (Δx piccolo).
più le lunghezza d’onda λi (velocità vi) sono diverse (Δv grande) più il pacchetto è concentrato (Δx piccolo).
Il rallentamento dell’onda (luce) si verifica nella rifrazione. La luce passando da un mezzo ad un altro con indice di rifrazione maggiore rallenta la sua velocità da c a c’ in quanto diminuisce la sua lunghezza d’onda da λ a λ’. In tal modo la sua frequenza di oscillazione v rimane costante: v = c/λ = c’/λ’. La luce quindi, anche se varia la sua velocità , non varia il suo numero di quanti h nell’unità di tempo, né la sua l’energia E = h*v =cost.
Finora abbiamo supposto onde (fotoni) con velocità diverse. Adesso, se ad ogni onda (fotone) con velocità ci accoppiamo l’onda gemella con velocità opposta -ci avremo l’onda stazionaria come sopra detto. Sarebbe in tal modo possibile ipotizzare un pacchetto costituito da un insieme di onde stazionare tutte con la stessa energia ma con lunghezze d’onda e velocità diverse. Si può altresì ipotizzare che tali onde stazionarie di uguali energie abbiano una distribuzione normale (gaussiana) nelle due dimensioni spazio-velocità (x,v). Tale pacchetto descriverebbe il comportamento dell’elettrone e spiegherebbe il principio di indeterminazione Δx*Δmv = h.
Si è visto come l’Azione può essere ottenuta come il prodotto di coppie di grandezze fisiche: Energia * Tempo, Quantità di moto * Spazio, Momento angolare * Rotazione, … Tali coppie sono definite come momenti coniugati e la relazione tra loro ha un profondo significato sul modo di interpretare la fisica:
- Il prodotto tra le lagragiane qi (energia, quantità di moto, momento angolare, …) e i rispettivi momenti coniugati pi dà la grandezza Azione;
- Nei fenomeni fisici, l’azione deve essere minima;
- L’energia è quantizzata;
- L’azione non può essere inferiore al quanto h di Planck;
- Un’onda di qualsiasi frequenza (ossia un’oscillazione singola) ha azione h;
Ritengo da ciò che in un esperimento fisico si possono/debbono misurare i quanti d’azione.
Riassumendo. Ritengo che la rappresentazione della particella come pacchetto di sole onde possa descrivere in modo adeguato il principio di indeterminazione e la complementarietà onda/corpuscolo. Con tale rappresentazione della particella risulta evidente che: più è facile rilevare l’aspetto corpuscolare più è difficile rilevare l’aspetto ondulatorio della particella. Si fa rilevare che la condizione necessaria affinchè il pacchetto d’onde sia stabile è che le sue onde debbano muoversi con velocità vi inversamente proporzionali alle loro frequenze vi: vi = 1/vi, cioè che sia verificata la relazione ∆x*m∆v = h.
Interpretazione della diffrazione di un elettrone con due fenditure. Nel caso della diffrazione con due fenditure l’elettrone singolo, essendo costituito da un pacchetto d’onde attraversa entrambi le fenditure e interferisce con sé stesso. Quando l’elettrone diffratto colpisce lo schermo può interagire con tale schermo solo per quantità unitarie di carica (nel caso di diffrazioni di fotoni per quantità unitarie di h), per cui si condensa/materializza come particella nel punto in cui è massima l’intensità dell’onda diffratta.
Osservando i punti in cui il fotone/elettrone interagisce con lo schermo, questi punti formano la figura di diffrazione. Il fotone/elettrone viene a colpire lo schermo come onda in fasi (tempi) sempre diverse. Più numerosi sono i fotoni/ elettroni, più sono le fasi dell’onda rappresentate, meglio viene rappresentata l’onda e il suo aspetto ondulatorio con la figura di diffrazione.
Ritengo che il passaggio dall’onda alla particella si possa paragonare ad un passaggio di stato da vapore (diffuso nello spazio) a liquido (concentrato in una goccia).
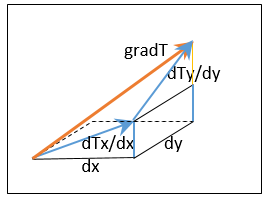 possono esprimersi con un solo valore e vengono dette grandezze scalari Tali grandezze associate ai punti dello spazio definiscono i campi scalari T(x,y,z). Le variazioni dello scalare dT al variare di dx, dy, dz cioè dTx/dx, dTy/dy, dTz/dz costituiscono il vettore gradiente F dello scalare T(x,y,z):
possono esprimersi con un solo valore e vengono dette grandezze scalari Tali grandezze associate ai punti dello spazio definiscono i campi scalari T(x,y,z). Le variazioni dello scalare dT al variare di dx, dy, dz cioè dTx/dx, dTy/dy, dTz/dz costituiscono il vettore gradiente F dello scalare T(x,y,z):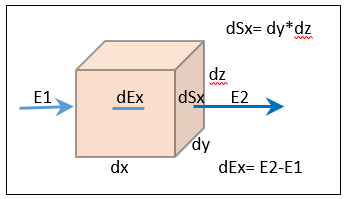
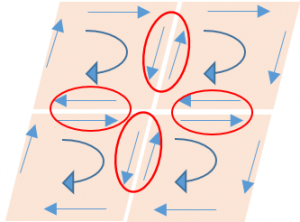
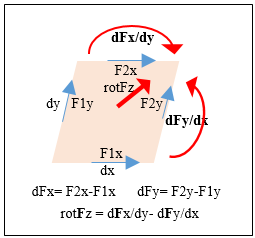 Dato un elementino di piano dx*dy e il campo vettoriale su tale piano cioè F(x,y) il vettore rotore rotFz per il piano (x,y) è la somma delle derivate dei 2 vettori sul piano lungo le 2 direzioni ad essi ortogonali: rotFz = dFx/dy – dFy/dx (7)
Dato un elementino di piano dx*dy e il campo vettoriale su tale piano cioè F(x,y) il vettore rotore rotFz per il piano (x,y) è la somma delle derivate dei 2 vettori sul piano lungo le 2 direzioni ad essi ortogonali: rotFz = dFx/dy – dFy/dx (7)