GRADIENTE di uno scalare = vettore
Molte grandezze fisiche (come la temperatura T, la pressione p, il potenziale elettrico V e gravitazionale U …) 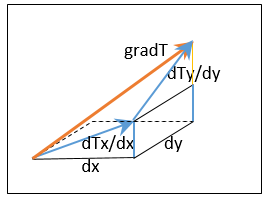 possono esprimersi con un solo valore e vengono dette grandezze scalari Tali grandezze associate ai punti dello spazio definiscono i campi scalari T(x,y,z). Le variazioni dello scalare dT al variare di dx, dy, dz cioè dTx/dx, dTy/dy, dTz/dz costituiscono il vettore gradiente F dello scalare T(x,y,z):
possono esprimersi con un solo valore e vengono dette grandezze scalari Tali grandezze associate ai punti dello spazio definiscono i campi scalari T(x,y,z). Le variazioni dello scalare dT al variare di dx, dy, dz cioè dTx/dx, dTy/dy, dTz/dz costituiscono il vettore gradiente F dello scalare T(x,y,z):
F(Fx,Fy,Fz) = – gradT(x,y,z) = – ∇T(x,y,z) = – (dTx/dx*i+dTy/dy*j+dTz/dz*k) (1)
da cui Fi*di = dTi (1a) ossia ∫ Fi*di = ∫dTi (1b) dove i = x,y,z
Il vettore gradiente è costituito dalle derivate dello scalare T rispetto alle ordinate spaziali dx, dy, dz. Se T(x,y) rappresenta la quota del terreno, il gradiente dTx/dx (dTy/dy) è la pendenza del terreno lungo dx (dy) mentre gradT dà la retta di max pendenza nel punto (x,y).
VETTORE E FLUSSO Molte grandezze fisiche (come la velocità, la forza, il campo elettrico e gravitazionale) vengono definite mediante vettori (costituiti da modulo, direzione e verso). Queste grandezze associate ad ogni punti dello spazio definiscono i campi vettoriali. Consideriamo una superficie infinitesima dS (ad esempio dSx = dy*dz) il FLUSSO che attraversa la superficie dSx è: Φx = Ex*dSx (2) mentre la quantità di flusso Ex che entra nel volume dv è dato dalla variazione di Ex lungo dx per la superficie dy*dz, cioè: dΦx = dEx*dSx (2a)
DIVERGENZA di un vettore = scalare
La derivata del vettore Ex lungo dx rappresenta la divergenza di E lungo x, cioè divEx = dEx/dx. La somma delle derivate lungo le diverse direzioni dà lo scalare divergenza del vettore E che è la variazione di E nell’elementino di volume dv = dx*dy*dz : 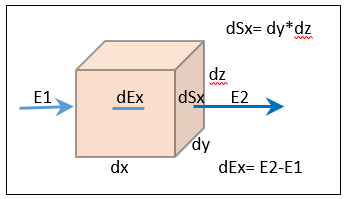
ρ(x,y,z) = divE = dEx/dx+dEy/dy+dEz/dz = ∇*E (3)
Se moltiplichiamo per dv la derivata in x: dEx/dx tale valore costituisce la variazione di flusso dentro dv di E lungo dx: dΦx = divEx*dv=dEx*dSx (4) (dove dSx = dy*dz). Il flusso totale nelle 3 direzioni vale:
dΦ = divE*dv = dE*dS = dρ/ε (4a)
La divE nel volume dv indica la presenza in dv di: sorgenti (cariche) se divE > 0 , pozzi se divE < 0. In altre parole la variazione di flusso dΦ all’interno di un volume dv di superficie dS dà la quantità di carica dρ racchiusa in tale volume. Ugualmente la divergenza divE nel volume v è uguale alla variazione di flusso E all’interno della superficie S del volume v: ∫divE*dv = ∫ (dEx/dx+dEy/dy+dEz/dz)*dv = ∫dEx*dy*dz+ ∫dEy*dx*dz+ ∫dEz*dx*dy = ∫dEx*dSx + ∫dEy*dSy + ∫dEz*dSz = ∫E*dS = Φs
ossia ∫divE*dv = ∫E*dS = Φs = ρ/ε (4b)
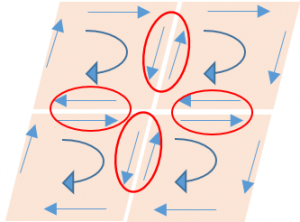
Considerato il volume v costituito da tanti cubetti dv la (4b) può essere spiegata osservando che i flussi che attraversano le facce interne danno un contributo nullo in quanto il flusso che esce da un elementino entra in quello successivo. Per cui il flusso totale è costituito solamente dal flusso che attraversa le facce esterne che compongono la superficie esterna S del volume v.
Combinando la (1) e la (2) si ha: divE = div*grad T = ∇²(T) = ρ/ε (5) (∇² = ∇*∇ è detto Laplaciano).
La (5) indica che un campo scalare (ad esempio la Temperatura) deve variare almeno con legge quadratica per contenere una sorgente di calore.
ROTORE di un vettore = vettore
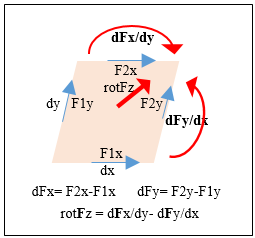 Dato un elementino di piano dx*dy e il campo vettoriale su tale piano cioè F(x,y) il vettore rotore rotFz per il piano (x,y) è la somma delle derivate dei 2 vettori sul piano lungo le 2 direzioni ad essi ortogonali: rotFz = dFx/dy – dFy/dx (7)
Dato un elementino di piano dx*dy e il campo vettoriale su tale piano cioè F(x,y) il vettore rotore rotFz per il piano (x,y) è la somma delle derivate dei 2 vettori sul piano lungo le 2 direzioni ad essi ortogonali: rotFz = dFx/dy – dFy/dx (7)
Considerando la circuitazione dell’elementino dA = dx*dy eseguita dal vettore F ossia Σ F*dl
Σ F*dl = F1x*dx- F2x*dx+ F2y*dy-F1y*dy = (F1x-F2x)*dx + (F2y-F1y)*dy = dFx*dx – dFy*dy che diviso per dA Σ F*dl/dA = rotF ossia rotF*dA = Σ F*dl (8a)
La (8) viene letta: il flusso del rotore F che attraversa l’area dA è uguale alla circuitazione dell’elementino dA da parte del vettore F .
In forma integrale la (8) si scrive ∫ rotF*dA = ∫ F*dl (8b)
Considerato la superficie A costituito da tanti quadratini dA la (8a) può essere spiegata osservando che i flussi che percorrono i lati interni danno un contributo nullo in quanto sono percorsi in senso inverso nel lato del quadratino adiacente, per cui la circuitazione totale è costituita solamente dai lati esterni cioè dalla curva che delimita la superficie A.
Teorema di Stokes Si osserva che con la ∫ Fi*di = ∫dTi (1b) si ha la relazione tra l’integrale di linea i e l’integrale dei punti (scalare) T estremi della linea l; con la ∫ rotF*dA = ∫ F*dl (8b) si ha la relazione tra l’integrale di superficie A e l’integrale di linea l contorno di A, con la ∫divE*dv = ∫E*dS (4b) si ha la relazione tra l’integrale di volume v e l’integrale di superficie S contorno di v. Il Teorema di Stokes descrive tutte e 3 le relazioni in quanto considera il legame tra l’integrale su una V-grandezza a (n)dimensioni e l’integrale su una S-grandezza a (n-1)dimensioni, in cui la S-grandezza è il contorno della V-grandezza. …