Polinomi. Se di una funzione y = f(x) conosciamo n punti (x1, y1); (x2, y2); …( xn, yn), la funzione più semplice che approssima la f(x) è il polinomio di grado n-1: Pn-1(x) = a0 + a1x + a2x2 + … + an-1xn-1 che passa per tali punti. Ad esempio, se si conoscono 2 punti si può scrivere il polinomio di grado 2-1 (equazione della retta) ed imporre la condizione che passi per tali punti, cioè il sistema di 2 equazioni con 2 incognite:
- a0 + a1 x1 = y1
- a0 + a1 x2 = y2
Trovati i valori delle incognite a0, a1, si può scrivere l’equazione della retta ossia il polinomio di 1° grado P1(x) : y = a0 + a1x (1) .
Se si conoscono n+1 punti possiamo scrivere un sistema di n+1 equazioni con n+1 incognite, calcolare le: a0, a1, … an e quindi : Pn(x) = a0 + a1x + … +anxn (2) Più punti della funzione y = f(x) si conoscono migliore è l’approssimazione del polinomio alla suddetta funzione.
Rappresentiamo, adesso, in figura gli addendi del polinomio P2(x) = a0 + a1x + a2x2 (si limita lo studio al polinomio di 2° per brevità di esposizione). I coefficienti ai hanno un significato fisico? Consideriamo l’Area del Polinomio (ossia l’area sottesa dal Polinomio tra 0 e x), il 1° addendo delimita un rettangolo di area A1= x*a0; il 2° addendo un triangolo di area : A2= x* a1*x/2, il 3° addendo una parabola di area A3= x*a2*x2/3. L’area totale è: A(x) = (a0+a1*x/2+a2*x2/3)*x.
Legge oraria. Se diamo alla funzione polinomiale il significato fisico della funzione accelerazione a(t) = P(t) si vuole calcolare lo spazio percorso da un punto nel tempo t. In figura (a) è rappresentata la funzione accelerazione a(t)= ao+a1*t. Posto t = t1 – t0 , l’area sottesa da a(t) con l’asse t dà la velocità v(t) = v2 +v3 = ao *t+ a1*t2/2 (3) 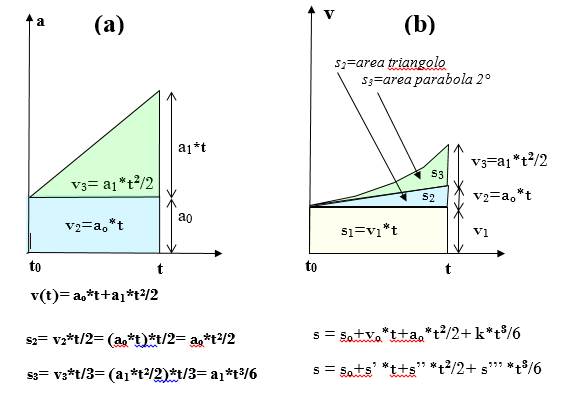
In figura (b) è rappresentata la funzione velocità v(t). L’area sottesa rappresenta lo spazio s(t) = so+vo*t+ao/2!*t2+ a1/3!*t3 (4) avendo indicato con so il valore iniziale. Si evidenzia che: vo rappresenta la velocità v all’istante t= 0 vo= ds/dt= s’o; ao l’accelerazione all’istante t= 0 ao = d2s/dt2= s”o …, per cui la (4) può essere riscritta con le derivate in un punto t, ossia come polinomio di Taylor : s(t) = so+s’o*t1+s”o/2!*t2 + s”’o/3!*t3 (4a)
Polinomio/Serie di Taylor. Tale serie, costituita appunto dai valori delle derivate della funzione f(x) in un punto (continua e derivabile in un punto x), approssimano la funzione f(x):
y(x) = y+y’ *(x – x0)+y’’/2!*(x – x0)2+ y’’’/3! *(x – x0)3 + …+ yn‘/n!*(x – x0)n (4b)
Polinomio/Serie di McLaurin. Se scegliamo x0=0 il suddetto polinomio diventa di McLaurin: y(x) = y(0)+y’(x)*x+y’’(x)/2!*x2+ y’’’(x)/ 3!*x3+ …+ yn’(x)/ n!*xn (4c)
Esempio: Data la funzione y(x) = 2*x 2 + x si vuole calcolare la Serie
di Taylor per x0=1.
Si ha: y(1) = 3, y’(1) = 4*x +1 = 5, y"(1) = 4.
y (x) = y + y’*Δx+y"*Δx2/2 = 3+5*Δx+4*Δx2/2 = 3+5*Δx+2*Δx2
Per x=2, Δx =x-x0= 1 P2(x=2) = 3+5*1+2*12 = 10.
Per x=3, Δx =x-x0= 2 P2(x=3) = 3+5*2+2*22 = 21.
La Serie di McLaurin: x0=0 , y(0) = 0, y’(0) = 1, y"(0) = 4
quindi y(x) = y(0)+y’(0)*x+y"(0)/2!*x2 = 0+1*x+4/2*x2 = 2*x2 + x.
Altro metodo per trovare gli ai. Consideriamo il polinomio Pn(x) = a0 + a1x + … +anxn come la somma di n funzioni yi(x) = aixi con. Calcoliamo il coefficiente ai derivando la y(x) i volte: y i’ = i!*ai da cui si ricavano i coefficienti ai = y i’ /i! della serie.
Nota: Se si eguagliano i termini della (2) e della (4b) si trovano i valori dei coefficienti ai: a0 =y, a1 =y’/1!, a2=y”/2!, … an=yn’/n!. Si osserva infatti che la derivata di ai*xi é: i*ai*xi-1 e che la derivata i-esima di ai*xi é : yi’ = i!*ai.