L’aberrazione della luce
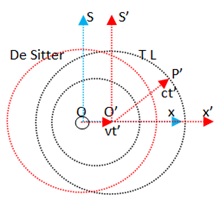
Supponiamo di essere fermi e che la pioggia cada verticalmente con una velocità c. 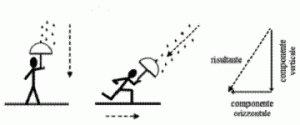 Se ci muoviamo con velocità v le due velocità si compongono per cui le gocce le vediamo arrivare alla velocità risultante r = (v²+c²) 1/2 = c*(1+v²/c²) ½ e con un angolo Ψ ≈ v/c rispetto alla verticale. Tale fenomeno viene chiamato aberrazione e Ψ angolo aberrazione.
Se ci muoviamo con velocità v le due velocità si compongono per cui le gocce le vediamo arrivare alla velocità risultante r = (v²+c²) 1/2 = c*(1+v²/c²) ½ e con un angolo Ψ ≈ v/c rispetto alla verticale. Tale fenomeno viene chiamato aberrazione e Ψ angolo aberrazione.
Il fenomeno dell’aberrazione si verifica anche con la luce. Se, ad esempio, vogliamo osservare le stelle poste sulla nostra verticale, dobbiamo inclinare il telescopio rispetto alla verticale di un angolo di aberrazione Ψ che tenga conto del moto della Terra attorno al Sole.
Le immagini riportate sono tratte dal sito Giornale di Astronomia – 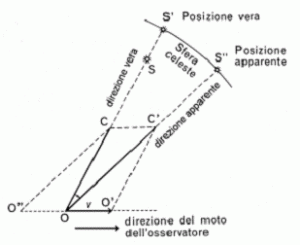 Spigolature Astronomiche: http://www.bo.astro.it/sait/spigolature/spigo103base.html
Spigolature Astronomiche: http://www.bo.astro.it/sait/spigolature/spigo103base.html
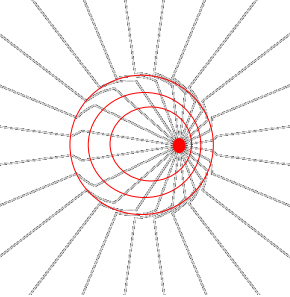
Il fenomeno fu scoperto da Bradley nel 1728 osservando la stella Egli si accorse che per osservare la stella doveva variare l’inclinazione del telescopio al variare della velocità v della Terra attorno al Sole. La direzione di tale inclinazione durante l’anno descrive un’ellisse. Bradley rilevò una “variazione” dell’angolo di aberrazione della luce pari a 20,50 secondi d’arco. Poiché 3600″(sec. d’arco) = 1°(grado) si ha 20″,50 = 0,00569° quindi tan(0,00569°) ≈ 0,0009937 = v/c. Per cui la velocità della Terra attorno al Sole risulta pari a v ≈ 29.8 km/s. 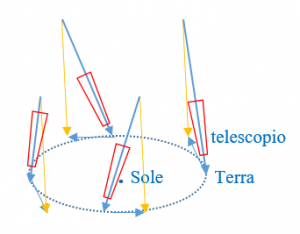 Tale angolo è relativo in quanto considera la “variazione” della velocità della Terra rispetto al Sole e non considera la velocità del sistema solare, … . Per cui il telescopio, per poter catturare i raggi, deve essere inclinato di un angolo di aberrazione che tenga conto della sua velocità “totale” (compresa quella del sistema solare …) rispetto alla direzione della luce.
Tale angolo è relativo in quanto considera la “variazione” della velocità della Terra rispetto al Sole e non considera la velocità del sistema solare, … . Per cui il telescopio, per poter catturare i raggi, deve essere inclinato di un angolo di aberrazione che tenga conto della sua velocità “totale” (compresa quella del sistema solare …) rispetto alla direzione della luce.
La direzione della luce di una stella (in arancione) durante l’anno non cambia in quanto molto lontana. Per l’osservatore sulla Terra come già detto tale direzione (in blu) varia a causa del moto della Terra. Il telescopio (in rosso), infatti, per catturare il raggio della stella sull’oculare deve variare la sua inclinazione. È evidente che se la velocità della Terra non variasse l’inclinazione del cannocchiale rimarrebbe uguale.
L’orologio a luce
Consideriamo, adesso, l’esperimento mentale dell’orologio a luce (l’immagine è tratta dal sito http://www.fmboschetto.it/tde/2_2.htm del Prof. Ing. F.M. Boschetto), che viene preso come esempio nella Relatività Speciale (RS) per spiegare il rallentamento relativo del tempo con l’aumento della velocità. 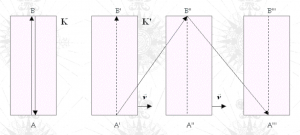
L’orologio a luce calcola, infatti, il tempo impiegato da un fotone a compiere il percorso di andata e ritorno tra i due specchi piani e paralleli A e B. Dati due di questi orologi K e K’ in quiete, i tempi impiegati dai fotoni evidentemente saranno uguali. Se l’orologio K’, invece, si mette in moto con velocità v rispetto all’orologio K, si ritiene che il tempo impiegato dal fotone sia maggiore in quanto si ritiene che esso compia un percorso in diagonale.
Secondo la RS invece, poiché non è possibile distinguere quale dei due orologi è in moto (i sistemi sono tutti uguali e indistinguibili), sussistono entrambi i casi: ossia per l’osservatore solidale con l’orologio K è l’orologio K’ a rallentare, mentre per l’osservatore solidale con l’orologio K’ è l’osservatore K a rallentare.
Osservazioni
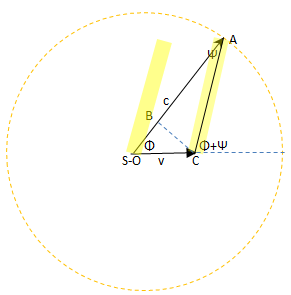
In verità, sull’esperimento dell’orologio a luce (o meglio a fotoni) (*) è necessario rilevare quanto segue. Se il fotone viene sparato in direzione verticale esso colpirà lo specchio superiore solo se l’orologio rimane fermo. Infatti, se tale fotone riuscisse a colpire lo specchio in moto tale evento dimostrerebbe il trascinamento del fotone da parte dell’orologio, che risulterebbe in contrasto col Principio della costanza della velocità della luce.
Il fotone, pertanto, dovrebbe colpire il punto B’’ distante dallo specchio di B’B’’ = A’B’ *v/c, (dove B’B’’ è la distanza percorsa dall’orologio nel tempo impiegato dal fotone a percorrere la distanza tra i due specchi). Pertanto, per colpire lo specchio in moto, il fotone dovrebbe essere sparato con un’inclinazione pari ad un angolo Ψ ≈ B’B’’/A’B’ = v/c, che corrisponde con l’angolo di aberrazione. L’esperimento dell’orologio a luce, per l’osservatore solidale all’orologio, deve essere interpretato come l’aberrazione del fotone, dove il moto verticale del fotone si combina con il moto orizzontale dell’orologio.
In pratica conoscendo l’angolo d’inclinazione (aberrazione) dei fotoni è possibile determinare la velocità dei due orologi K e K’. L’orologio K si potrà considerare realmente fermo se il fotone, sparato con direzione verticale, colpirà lo specchio superiore, mentre l’orologio K’ si potrà considerare realmente in moto con velocità v se il fotone sparato con inclinazione Ψ ≈ v/c colpirà lo specchio superiore.
Pertanto gli orologi (sistemi) non possono ritenersi tutti uguali e indistinguibili (come ipotizza la RS) ma ognuno con una propria velocità rispetto al fotone. Risulta indispensabile, allora, definire il sistema di riferimento assoluto (con velocità nulla), come quel sistema in cui l’aberrazione dei fotoni è nulla in tutte le direzioni. Un sistema che, essendo composto da fotoni, possiamo chiamare “sistema luce”.
(*) E’ più corretto parlare di orologio a fotone o a lampi di luce, invece che di orologio a luce, al fine di avere “proiettili” che siano indipendenti dal moto della sorgente. Infatti mentre il fotone una volta emesso percorre una linea retta, il raggio di luce essendo costituito da un insieme di fotoni emessi dalla sorgente uno dopo l’altro in tempi diversi può avere una linea curva se la sorgente è in moto. Si veda https://www.motionmountain.net/motionmountain-volume2-it.pdf esempio del faro pag. 19 e 20.
Conclusioni
L’orologio a luce è un esempio valido per spiegare la dilatazione del tempo solo se lo si interpreta come un fenomeno di aberrazione. Tale fenomeno però implica l’esistenza di un sistema assoluto, che contraddice il 2° postulato della relatività. D’altra parte, se si dovesse ritenesse nulla l’aberrazione dei fotoni si dovrebbe concludere che la velocità della luce non sia costante.
Si deve concludere che la Teoria della RS, sebbene fornisca valori pressoché uguali a quelli sperimentali, ciò grazie alla velocità trascurabile del nostro sistema Terra (circa 3.000 km/sec) rispetto alla velocità della luce, non sia valida sotto l’aspetto epistemologico (ossia come metodo scientifico).