Ing. Giovanni Colletti
Articolo completo pubblicato su Academia.edu: Spazio e tempo assoluti senza il 2 ° postulato della Relatività. Le leggi fisiche sono invarianti rispetto alla Luce
PREMESSA
Se consideriamo gli atomi di un corpo, essi si trovano a una distanza tale che le forze (coulombiane) di attrazione e repulsione sono tra loro in equilibrio. Questa distanza si chiama distanza di legame e determina la dimensione del corpo. Se consideriamo le equazioni delle forze coulombiana F= k*qQ/r² e delle forze gravitazionali F = G*Mm/r² si osserva che la propagazione di tali forze è stata considerata istantanea in quanto in esse non è presente il tempo. Tale propagazione ha in realtà una velocità uguale a quella della luce, per cui a una distanza r la perturbazione arriva dopo il tempo t= r/c. Se il corpo è in movimento tale tempo (ritardo), come vedremo, aumenta e con esso variano le forze di legame e le dimensione del corpo (distanza di legame). Questo avviene ovviamente sia per le forze coulombiane sia per le forze gravitazionali. Risulta importante quindi capire rispetto a cosa il corpo è in movimento. [1] In questo articolo si intende studiare allora, il comportamento dei corpi in movimento tenendo conto che la velocità di propagazione delle interazioni è uguale alla velocità della luce. A tal fine si farà riferimento soprattutto all‘esperimento di Michelson e Morley, e al comportamento delle aste dell’interferometro al variare della velocità. Saranno utilizzati dei principi validati dagli esperimenti, per cui non sarà utilizzato il 2° postulato della TdR, al fine di dare una interpretazione oggettiva (reale) del fenomeno. Le Trasformazioni di Lorentz infatti, proprio perché contengono tale postulato, non possono dare una interpretazione oggettiva delle grandezze fisiche (spazio e tempo) ma relativistica. Con i suddetti principi, dopo avere distinto i vari esperimenti (secondo il n° di sistemi di riferimento e secondo i percorsi compiuti dalla luce: di solo andata o di andata e ritorno) si passa ad esaminarli. Infine vengono presentati alcuni esperimenti con i quali si ritiene possibile calcolare la velocità assoluta dei sistemi.
[1] Riguardo le proprietà del vuoto e la velocità di interazioni delle forze F si ritiene interessante il filmato del prof. Adriano Morando Spazio Tempo e Materia.
Riguardo i corpi in movimento si citano gli Appunti del corso di Fisica Teorica – del Prof. Pierantonio Zanghi pag. 34, in cui risulta che i potenziali ritardati (campi di forza) nello spazio presentano una “contrazione” nella direzione del moto.
-
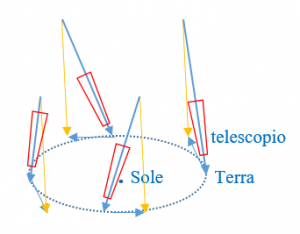
L’esperimento di Michelson e Morley e la Teoria della Relatività
L’esperimento di MM è stato ideato per dimostrare l’esistenza dell’etere. A ciascuno dei 2 raggi di luce si fanno percorrere, in andata e ritorno, bracci diversi di un interferometro disposti uno lungo la direzione del moto l’altro nella direzione ortogonale. Poiché si riteneva che l’etere nel suo moto trascinasse la luce, con tale esperimento si cercava di osservare (in periodi diversi dell’anno, essendo l’interferometro in moto con la Terra attorno al Sole, o ruotando l’interferometro) un fenomeno di interferenza che avrebbe provato il ritardo di uno dei due raggi. Con qualsiasi rotazione dello strumento e in qualsiasi periodo dell’anno, tuttavia, non è stata osservata alcuna interferenza. L’esperimento, se per un verso era fallito, dimostrava comunque che i raggi di luce in un percorso di andata e ritorno impiegano lo stesso tempo qualunque sia la velocità del corpo (interferometro). Per spiegare tale strano fenomeno Lorentz ipotizzò che il movimento generasse una contrazione “reale” nei corpi lungo la direzione del moto. A tale ipotesi Einstein affiancò la sua: la velocità della luce è uguale in tutti i sistemi in moto (2° postulato della Teoria della Relatività). Tale postulato ipotizza che il tempo impiegato dalla luce per raggiungere un corpo non dipende dalla velocità del corpo, in altre parole che in un sistema inerziale (in moto con velocità costante) i tempi impiegati dalla luce nei percorsi di andata sono uguali a quelli di ritorno .
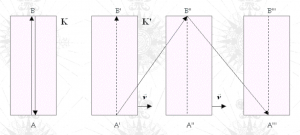
1.1 Le Trasformazioni di Lorentz (TL) Come il suono ha bisogno dell’aria per propagarsi, si riteneva che anche la luce avesse bisogno dell ‘ etere per propagarsi. Il fenomeno dell’aberrazione stellare, l’esperimento di Fizeau e l’esperimento di Michelson e Morley davano risultati contrastanti riguardo il comportamento della velocità della luce nell’etere. Dopo diverse interpretazioni le Trasformazioni ideate da H.Lorentz, ipotizzando la deformazione del corpo lungo la direzione del moto, riuscivano a spiegare tali risultati contrastanti. Nella creazione di tali Trasformazioni, tuttavia, è stata ipotizzata la costanza della velocità della luce in percorsi di solo andata (2° postulato), (vedi youmath Dimostrazione del calcolo delle TL), nonostante l’esperimento di MM dimostrasse la costanza della velocità della luce in un percorso di andata e ritorno. Inoltre, poiché l’esperimento di MM è costituito da un solo sistema (osservatori – interferometro), per poter applicare tali Trasformazioni è necessario considerare un altro sistema di riferimento per determinare la velocità dell’interferometro. L’interazione che avviene esclusivamente tra l’interferometro e la luce (a parere dello scrivente) viene ad essere pertanto “inquinata” dall’inserimento di un altro sistema estraneo al fenomeno. Per tale ragione si definisce una velocità “relativa” dell’interferometro (in quanto riferita al nuovo sistema) e una deformazione relativa dello spazio e del tempo. Accettare le TL implica ritenere valida la “simmetria della relativa“, cioè: considerati due sistemi A e B fra loro in moto, ritenere validi sia la contrazione di B per l’osservatore A, sia la contrazione di A per l’osservatore B. Voler dare, quindi, con le TL (ossia con la TdR) un significato reale alle deformazioni dello spazio e del tempo risulta pura fantasia. Con il 2° postulato si deve quindi rinunciare alla possibilità di definire uno spazio e un tempo reali, ossia di descrivere il reale comportamento della materia in movimento. Tale situazione si ritiene insostenibile (inaccettabile) se si considera che l’introduzione del 2° postulato nella creazione delle TL non è stata obbligatoria ma ”opportuna”. L’utilizzo del 2° postulato viene consigliato da Poincarè per dare alla teoria fisica la forma più semplice (da Wikipedia): ”(Poincaré) … trattò la difficoltà di stabilire la simultaneità a distanza e concluse che si potesse stabilire per convenzione. Egli asserì anche che gli scienziati dovevano porre la costanza della velocità della luce come postulato per dare alla teoria fisica la forma più semplice.”
Considerato quanto sopra, per una lettura oggettiva dell’esperimento di Michelson e Morley si ritiene necessario:
- Leggere l’esperimento di MM come una interazione tra il corpo e la luce;
- Considerare la costanza del tempo, impiegato dalla luce per percorsi di andata e ritorno, lungo qualsiasi direzione una Proprietà della natura.
1.2 Il 2° postulato: un’ipotesi imbarazzante. Sebbene le impostazioni sopra indicate per interpretare l’esperimento di MM siano diverse, si ritiene utile richiamare l’articolo TEMPO RELATIVO E SIMULTANEITÀ ASSOLUTA del Prof. Franco Selleri. In esse si mette in discussione il 2° postulato. Si riportano alcuni passaggi in cui si coglie l’imbarazzo nei confronti di tale postulato e di conseguenza delle TL e della TdR.
Dal paragrafo 2. Il totale relativismo di cui la teoria sembrerebbe portatrice è un’illusione. Insomma non tutto è relativo nella relatività: essa contiene anche qualcosa che relativo non è, qualcosa di assoluto! Come scriveva il fisico Helbert Dingle: “Dovrebbe essere ovvio che se c’è un effetto assoluto che è funzione della velocità, allora la stessa velocità deve essere assoluta. Nessuna manipolazione di formule e nessun concepimento di ingegnosi esperimenti può alterare questo semplice fatto.” .
Dal paragrafo 3. Una domanda che sembra legittima è: “Ma cosa succede realmente al regolo, qual’è la sua vera lunghezza?” La risposta relativistica è che la domanda non ha alcun senso e che i punti di vista di tutti i diversi osservatori  sono egualmente, anche se limitatamente, validi. E’ la filosofia del relativismo e del soggettivismo che si afferma in fisica per le tipiche constatazioni degli osservatori in moto. – Ehrenfest sentì molto acutamente l’esistenza di questo genere di problemi. La teoria di relatività speciale basata sulla negazione dell’etere richiede la completa equivalenza degli osservatori in moto relativo uniforme, perché non c’è ragione che siano inequivalenti, dato che si muovono rispetto al nulla. Tuttavia se si adotta il principio d’equivalenza che Einstein formulò nel 1916 e su cui basò la teoria di relatività generale, si conclude che l’inerzia ha la sua origine negli effetti gravitazionali delle masse lontane, effetti mediati da campi fisici presenti nello spazio vuoto. Ma la parola etere e la parola campo indicano all’incirca la stessa cosa, un vuoto dotato di proprietà fisiche. Questa contraddizione angustiava Ehrenfest che nel 1919 scrisse ad Einstein: “Ora non si può più dire che si muovono rispetto al nulla, perché si muovono rispetto a un enorme qualcosa! … Einstein, il mio stomaco disturbato odia la tua teoria – quasi odia anche te! Come posso educare i miei studenti? E cosa posso rispondere ai filosofi?!!”
sono egualmente, anche se limitatamente, validi. E’ la filosofia del relativismo e del soggettivismo che si afferma in fisica per le tipiche constatazioni degli osservatori in moto. – Ehrenfest sentì molto acutamente l’esistenza di questo genere di problemi. La teoria di relatività speciale basata sulla negazione dell’etere richiede la completa equivalenza degli osservatori in moto relativo uniforme, perché non c’è ragione che siano inequivalenti, dato che si muovono rispetto al nulla. Tuttavia se si adotta il principio d’equivalenza che Einstein formulò nel 1916 e su cui basò la teoria di relatività generale, si conclude che l’inerzia ha la sua origine negli effetti gravitazionali delle masse lontane, effetti mediati da campi fisici presenti nello spazio vuoto. Ma la parola etere e la parola campo indicano all’incirca la stessa cosa, un vuoto dotato di proprietà fisiche. Questa contraddizione angustiava Ehrenfest che nel 1919 scrisse ad Einstein: “Ora non si può più dire che si muovono rispetto al nulla, perché si muovono rispetto a un enorme qualcosa! … Einstein, il mio stomaco disturbato odia la tua teoria – quasi odia anche te! Come posso educare i miei studenti? E cosa posso rispondere ai filosofi?!!”
Dal paragrafo 4. D’altra parte egli (Einstein) dimostrò in più occasioni di avere ben chiaro il carattere convenzionale del postulato di invarianza della velocità della luce, ad esempio nel 1916 scrivendo a proposito del punto mediano M di un segmento AB gli estremi del quale sono colpiti “simultaneamente” da due fulmini: “Il fatto che la luce impieghi lo stesso tempo per percorrere AM e BM è solo una convenzione arbitrariamente stabilita per ottenere una definizione di simultaneità, e non un’ipotesi sulla natura della luce sotto l’aspetto fisico.” … Ovviamente se una affermazione scientifica è vera non si può che accettarla, ma se è solo convenzionale diventa invece interessante la ricerca di alternative basate su convenzioni diverse da quella normalmente usata. In particolare, se la costanza della velocità della luce è una pura convenzione priva di base empirica deve essere legittimo studiare teorie in cui tale costanza non vale. Ma nel fare questo si violerà anche il principio di relatività, almeno nella sua accezione forte, quella usata per dedurre le trasformazioni di Lorentz. Questo può solo significare che lo stesso principio di relatività è almeno in gran parte un’utile convenzione umana e non un fatto della natura. Infatti una “verità” riconosciuta come convenzionale (la costanza della velocità della luce) non potrebbe essere conseguenza necessaria del principio di relatività se questo fosse una proprietà oggettiva della natura. Premesse oggettive possono solo portare a conseguenze altrettanto oggettive!
Dal paragrafo 5. La simultaneità assoluta.
Si ritiene inoltre opportuno riportare i seguenti, a parere dello scrivente, paradossi :
- Ipotizziamo due particelle A e B aventi la stessa età in avvicinamento con velocità relativistica v. Quando sono vicinissime si può ipotizzare che: caso 1. Sia la particella A a frenare e fermarsi accanto alla particella B; caso 2. Sia la particella B a frenare e fermarsi accanto alla particella A. Per la TdR nel caso 1 è la particella A a rimare giovane in quanto la B è rimasta ferma; nel caso 2 è la particella B a rimanere giovane in quanto la A è rimasta ferma. Per la TdR entrambi i casi sono possibili, per cui si dovrebbe concludere che sia la variazione di velocità a far rimanere giovane una particella rispetto all’altra. Ma la stessa TdR, prevede che sia il tempo trascorso da una particella quando viaggia a una velocità maggiore a farla rimanere giovane rispetto all’altra.
- Se per un verso la Teoria della Relatività considera i sistemi di riferimento tutti uguali, dall’altro il 2° postulato ipotizza la velocità della luce uguale per tutti i sistemi di riferimento. Cioè la luce si ritiene una entità unica per tutti i sistemi. Considerando allora la luce come un sistema particolare dobbiamo dedurre che la TdR (basandosi sul 2° postulato) contenga una contraddizione. In sostanza la TdR può esprimersi con la frase: “Tutti i sistemi di riferimento sono uguali in quanto fanno tutti riferimento al sistema luce“. Tale frase si ritiene contenga una contraddizione, essa è del tipo: “Io dico sempre bugie”. Se riflettiamo su tale frase ci accorgiamo che essa non può essere considerata vera ma nemmeno falsa, essa infatti contiene una “contraddizione” cioè risulta indecidibile (indeterminabile). Consideriamo adesso il 1° Teorema di incompletezza di Gödel: “Una teoria è incompleta se non riesce a dimostrare una formula indecidibile”, la TdR basandosi sulla frase indecidibile sopra riportata risulta allora completa. Consideriamo adesso il 2° teorema di incompletezza di Gödel: “Nessun teoria coerente (essendo incompleta) può dimostrare la sua stessa coerenza”. Per tale teorema allora la Teoria della Relatività risulta completa in quanto contiene il 2° postulato e, poiché lo considera vero, anche incoerente. Per quanto sopra detto la Teoria della Relatività non si ritiene dimostrabile né confutabile in quanto indecidibile e incoerente.
Un incongruenza si coglie, altresì, tra la Teoria della Relatività (TdR) e la Relatività Generale (RG). Il principio di equivalenza tra massa gravitazione e massa inerziale richiede una definizione concreta di massa inerziale che non può essere identificata con la massa a riposo della TdR. Quest’ultima infatti dipendente dal sistema di riferimento scelto. Per sistemare (a parere dello scrivente in modo maldestro) tale “inconveniente” è stata definita la massa invariante m ad ogni velocità v<c.(???) (si veda la definizione di massa invariante su Wikipedia). Secondo tale definizione dovrebbe esistere una massa invariante per ogni sistemi di riferimento? Ma se è invariante non dovrebbe essere valida per tutte le velocità? La Teoria della RG, con la geometrizzazione, del campo gravitazionale richiede l’esistenza di una massa inerziale non ambigua.
1.3 Le Trasformazioni Inerziali. Come si è detto sopra, l’applicazione del 2° postulato nelle TL è stata una scelta di comodo, la più semplice, tuttavia non suffragata da esperimenti. Diverse solo le Trasformazioni proposte che non applicano il 2° postulato. Tra esse quella particolarmente interessante e la Trasformazione Inerziale, che considera un sistema di riferimento assoluto in cui la luce risulta isotropa, cioè con velocità uguale in tutte le direzioni (per cui l’effetto Doppler è nullo) e dove il tempo e lo spazio sono assoluti. Vedremo come, utilizzando l’esperimento di Michelson e Morley, è possibile ricavare in maniera elementare trasformazioni analoghe a quelle Inerziali.
-
Le Proprietà della Luce per una nuova Teoria
Per l’interpretazione dell’esperimento di Michelson e Morley utilizziamo le seguenti proprietà della luce:
- La velocità della luce non dipende dalla velocità della sorgente [2].
- Per ogni SRI la luce nei percorsi chiusi (di andata e ritorno) ha una velocità costante in tutte le direzioni [3] .
La 1° proprietà ha una profonda implicazione per le trasformazioni galileiane. G. Galilei si rese conto che all’interno di un sistema in moto con velocità costante non è possibile rilevare la velocità del sistema, da ciò dedusse che le leggi fisiche sono uguali in tutti i sistemi con velocità costante (Inerziali). Ciò risulta vero per tutti i fenomeni meccanici tranne per la luce. Essa, infatti, non viene trascinata dal sistema dentro cui si trova, in quanto la sua velocità, come scoperto da Maxwell, è costante. Tale proprietà della luce si ritiene possa essere utilizzata per determinare la velocità “assoluta” del sistema.
Definite le proprietà della luce è necessario fare una distinzione dei fenomeni in base:
- al numero di Sistemi di Riferimento Inerziali 1 o 2 SRI;
- al percorso effettuato dalla luce: solo andata o andata e ritorno.
[2] Brecher, K. (1977), “La velocità della luce è indipendente dalla velocità della sorgente” , 10.1103 / PhysRevLett .39.1051
[3] Test di andata e ritorno di isotropia alla velocità della luce . Hils and Hall, Phys. Rev. Lett. 64 (1990), pag. 1697. simile a Brillet e Hall (sopra), Nessuna variazione è stata trovata al livello di 2-10 −13. I test corrispondono approssimativamente all’esperimento di Michelson-Morley
2.1 Definizione del Sistema Luce.
Consideriamo più corpi (sistemi) con velocità diverse e supponiamo che in un dato istante si trovino nello stesso punto. Se da tale punto ciascun sistema emette dei raggi (lampi) di luce, poiché la velocità della luce non dipende dalle velocità delle sorgenti (1a proprietà), questi raggi risulteranno indistinguibili per i sistemi in moto, ossia ciascun sistema vedrà i raggi tutti uguali. E’ possibile allora identificare questi raggi con un sistema, che possiamo chiamare Sistema Luce, che risulterà unico per tutti i sistemi. Tale sistema può essere realizzato quindi emettendo lampi di luce in tutte le direzioni. Un sistema sarà solidale al Sistema Luce se la velocità della luce risulterà isotropa, cioè con velocità uguale in tutte le direzioni (si fa rilevare che, non considerando valido il 2° postulato, per i sistemi in moto la luce assume velocità diverse da c).
3. Spazio e Tempo assoluti
3.1 Definizione di Spazio e Tempo. Consideriamo le 2 proprietà della luce sopra riportate e supponiamo che siano nulle le deformazioni del corpo nella direzione ortogonale al moto, per un sistema in moto possiamo definire:
- il tempo unitario come il tempo impiegato dalla Luce a percorrere in andata e ritorno uno spazio unitario nella direzione ortogonale al moto;
- lo spazio unitario lungo una direzione come lo spazio percorso in andata e ritorno dalla luce lungo tale direzione nel tempo unitario.
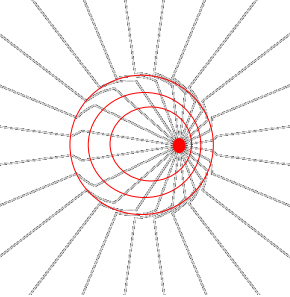
3.2 Spazio Tempo e Sfere in moto. L’esperimento della sfera in moto si può ritenere un esperimento di MM “generalizzato”, in quanto si può considerare costituito da diversi bracci disposti in diverse direzioni e dove vengono emessi lampi di luce in tutte le direzioni. Questi bracci naturalmente avranno una estremità in un centro comune e l’altra estremità su una circonferenza (o, se vogliamo, sulla superficie di una sfera) di raggio r=1. Nel filmato Sfera in moto si possono osservare dei raggi (lampi) di luce che partono dal centro F e ritornano al centro dopo avere toccato le pareti della sfera. Si fa rilevale che la sfera in moto (rossa) è contratta nella direzione del moto in modo che tutti i raggi arrivano al centro F’ della sfera nello stesso istante. 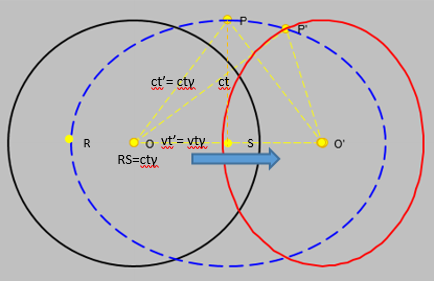 Si fa notare che i raggi di luce (per la proprietà dell’ellisse) percorrono distanze uguali in quanto partono da un fuoco e arrivano all’altro fuoco dell’ellisse blu (chiamata ellisse d’aberrazione in quanto dovuta all’aberrazione dei raggi a causa del moto). Gli stessi lampi di luce si muovono inoltre all’interno dell’ellisse rossa. Nella figura viene “fotografato” l’istante in cui un lampo di luce tocca le due ellissi nel punto P’. Si fa notare che nella sfera in moto i lampi di luce non arrivano nello stesso istante come nella sfera ferma. Se indichiamo con t =r/c ed L=c*t il tempo e lo spazio percorso dai raggi di luce nella sfera ferma, applicando il teorema di Pitagora al triangolo rettangolo OPS : OP² – OS² = PS² cioè (c*t)² = (c*t’)² – (v*t’)² si ricava il tempo t’ impiegato e lo spazio L’ percorso dai raggi di luce per la sfera (osservatore) in moto con velocità v:
Si fa notare che i raggi di luce (per la proprietà dell’ellisse) percorrono distanze uguali in quanto partono da un fuoco e arrivano all’altro fuoco dell’ellisse blu (chiamata ellisse d’aberrazione in quanto dovuta all’aberrazione dei raggi a causa del moto). Gli stessi lampi di luce si muovono inoltre all’interno dell’ellisse rossa. Nella figura viene “fotografato” l’istante in cui un lampo di luce tocca le due ellissi nel punto P’. Si fa notare che nella sfera in moto i lampi di luce non arrivano nello stesso istante come nella sfera ferma. Se indichiamo con t =r/c ed L=c*t il tempo e lo spazio percorso dai raggi di luce nella sfera ferma, applicando il teorema di Pitagora al triangolo rettangolo OPS : OP² – OS² = PS² cioè (c*t)² = (c*t’)² – (v*t’)² si ricava il tempo t’ impiegato e lo spazio L’ percorso dai raggi di luce per la sfera (osservatore) in moto con velocità v:
t’ = t/γ L’ = L*γ (1a) con γ = (1-v²/c²)½
Si fa rilevare che i coefficienti di deformazione del tempo t’ e dello spazio L’ sono uguali a quelli delle Trasformazioni di Lorentz. Tuttavia, mentre nelle TL la velocità v è relativa a 2 SRI, nelle relazioni (1a) la velocità v del sistema sfera viene riferita rispetto al Sistema Luce. Per tale motivo la suddetta velocità, come le deformazioni dello spazio L’ e del tempo T’, si può considerare reale. L’esempio della sfera in moto, con le relazioni (1), chiarisce (a parere dello scrivente) come lo spazio e il tempo dipendano esclusivamente dalla velocità del sistema e dalla velocità della luce. Si rileva che l’interazione tra particelle è composta da un percorsi di andata e ritorno della luce, come se le particelle comunicassero fra loro mediante raccomandate a.r. Riassumendo il rallentamento del tempo e la contrazione della lunghezza nella direzione del moto è causata dal maggior tempo impiegato dalla luce a percorrere la sfera in movimento.
E’ possibile ricavare facilmente le trasformazioni per passare dal sistema fermo (assoluto) al sistema in moto: x’ = (x-vt)*γ , y’=y , z’=z , t’ = t/γ (1) in cui γ = (1-v²/c²)½ x, y, z, t sono le coordinate assolute e le x’, y’, z’, t’ sono le coordinate per il sistema in moto. Da esse si ricavano: Δx’= Δx*γ, Δy’= Δy, Δz’= Δz, Δt’= Δt/γ (2)
Si fa rilevare che le Trasformazioni Assolute (1) coincidono con le Trasformazioni inerziali ottenute con 2 sistemi di riferimento e facendo coincidere un sistema col sistema inerziale (ossia col nostro Sistema Luce). Ossia le Trasformazioni di Lorentz risultano uguali alle Trasformazioni Assolute (1) solo se uno dei sistemi ha velocità nulla rispetto al Sistema Luce. Si può definire in maniera univoca allora la velocità, il tempo di ogni sistema facendo riferimento al Sistema Luce. Per mettere direttamente in relazione due sistemi in movimento è necessario conoscere le loro reali velocità
Si rimanda alle Trasformazioni inerziali proposte da altri studiosi per la definizione delle altre grandezze. L’esperimento della sfera oltre a offrire una rappresentazione realistica della dilatazione del tempo e della contrazione del corpo, sembra offrire anche la rappresentazione di altre grandezze fisiche che comunque devono essere verificate sperimentalmente.
3.3 Interpretazione delle ellissi. Per l’osservatore in moto l’intervallo di tempo impiegato dai tali raggi può considerarsi l’unità di tempo mentre lo spazio percorso può considerarsi l’unità di spazio. Se si ipotizza l’ellisse rossa proporzionale alla dimensione del corpo e l’ellisse blu proporzionale all’energia totale del corpo in quanto l’area percorsa dai raggi di luce, si possono avanzare le seguenti interpretazioni:
- Per velocità non relativistiche v<<c non si hanno deformazioni dello spazio e del tempo per cui l’Energia totale (ellisse blu) è costituita dall‘Energia a riposo (ellisse rossa) E=Eo. Inoltre, poiché i raggi di luce hanno uguali velocità, uguali direzioni di andata e ritorno ma verso opposto, è possibile considerare tali coppie di raggi come onde stazionarie la cui energia a riposo è costituita dall’energia cinetica interna Eo= Ec= 2*(½ k*c²) in cui k ha le dimensioni di una massa, ossia Eo= mc²;
- Per velocità relativistiche v ≤c si hanno le deformazioni dello spazio e del tempo per cui l’Energia totale E= moc²/γ (ellisse blu) aumenta mentre l’Energia a riposo (ellisse rossa) diminuisce E’o=moc²γ fino ad annullarsi per v=c. La differenza delle energie (ellissi blu – rossa) può ipotizzarsi come l’Energia cinetica Ec = moc²/γ – moc²*γ = moc²(1/γ-γ)= moc²(1-γ²)/γ = mov²/γ. Essa risulta nulla per v= 0 ed aumenta in maniera graduale con la velocità, fino ad assumere il valore infinito per v= c. Con le suddette interpretazioni delle ellissi un aumento della velocità produce una contrazione del corpo sino ad annullarsi, un rallentamento del tempo sino a fermarsi, un’espansione (del percorso) della luce sino a riempire tutto lo spazio. Ossia il corpo all’aumentare della velocità sembra perdere gradualmente l’aspetto corpuscolare e assumere l’aspetto ondulatorio. Secondo la Teoria della Relatività, invece, l’energia a riposo rimane costante.
3.4 Sistema Terra e Sistema Luce. Se si considera inattendibile il 2° postulato e con essa la Teoria della Relatività perché tale teoria ha ottenuto tante conferme sperimentali? La spiegazione (a parere dello scrivente) è che la velocità del nostro sistema Terra pari a 300 km/s circa non è relativistica (velocità calcolata rispetto alla radiazione cosmica di fondo, dove si è osservato un debole ma evidente effetto Doppler) . Tale velocità produce una deformazione trascurabile (con γ = 0,9999995), per cui il Sistema Terra può approssimarsi al Sistema Luce e le Trasformazioni di Lorentz possono approssimarsi alle trasformazioni (1) del paragrafo 3.2. Solo in tal modo è possibile dare un significato reale a tutte le velocità delle stelle, delle galassie, alla massa a riposo e all’energia dell’universo …
L’informazione: unità di misura di Spazio e Tempo. Considerato che la velocità della luce è unica per tutti i sistemi inerziali e che le informazioni si trasmettono con tale velocità possiamo dare le seguenti interpretazioni di spazio e tempo per tutti i sistemi inerziali:
- Il Tempo proprio di un sistema rappresenta la velocità con cui vengono scambiate le informazioni al suo interno;
- Lo Spazio proprio di un sistema è tale che lo scambio di informazioni al suo interno avviene nello stesso tempo in tutte le direzioni;
- L’energia unitaria in un sistema è la quantità di energia necessaria per scambiarsi una informazione;
- Le equazioni che esprimono le leggi della natura sono invarianti rispetto al tempo proprio e allo spazio proprio del sistema.
3.5 Una Teoria reale. La teoria, in quanto fondata sulle proprietà della luce, spiega senza paradossi il comportamento della natura. Il Sistema Luce costituisce l’unico sistema di riferimento. Tutti i sistema inerziale vengono “misurati” nel tempo e nello spazio tramite la velocità della luce. Vengono recuperati il Tempo assoluto e lo Spazio assoluto. Il rallentamento del tempo e la contrazione dello spazio sono considerati effetti reali dipendenti dalla velocità del sistema rispetto al sistema privilegiato. Al vuoto viene riconosciuta la proprietà di scambiare informazioni. . Con la nuova teoria la luce determina il ritmo reale del tempo e la dimensione reale dello spazio dei corpi in funzione della loro velocità. Due Sistemi possono relazionarsi tra loro tramite il sistema luce. Riguardo l’attendibilità della nuova Teoria tutti i fenomeni “relativistici” vengono calcolati in modo simile e con lo stesso ordine di precisione della TdR, ma con una interpretazione reale della deformazione dello spazio e del tempo quindi senza i paradossi della relatività. Inoltre interpreta senza contraddizioni altri fenomeni come l’effetto Sagnac, dove la TdR ha trovato difficoltà.
4. La Velocità Assoluta di un Sistema
4.1 Percorsi UNIDIREZIONALI della Luce. Secondo l’interpretazione fin qui espressa la deformazione dello spazio e del tempo dipenderebbe dalla velocità assoluta del sistema rispetto al Sistema Luce. per cui è necessario determinare tale velocità v. L’esperimento di MM, sebbene utilizzi un solo SRI, non è idoneo a determinare la velocità v del sistema in quanto i 2 raggi di luce, compiendo percorsi di andata e ritorno, arrivano contemporaneamente. Affinché gli esperimenti siano idonei si ritiene che, oltre ad essere costituiti da un solo sistema, i raggi di luce devono compiere percorsi unidirezionali. Due di essi sono l’esperimento di Sagnac, e l’aberrazione cinematica della luce.
4.2 L’esperimento di Sagnac. E’ un Sistema (non inerziale) costituito da un disco in rotazione con velocità ω, di raggio R e due raggi di luce che percorrono i bordi del disco in senso opposto. I raggi partono da un punto A del bordo del disco e arrivano al punto B diametralmente opposto ad A. Se il disco è fermo (ω =0) i raggi arrivano in B entrambi dopo un tempo t =π*R/c. Se il disco ruota i tempi impiegati dai 2 raggi sono diversi: per quello che va incontro a B risulta minore: t1 = π*R/(c+Rω) (1a) per l’altro che rincorre B risulta maggiore: t2 = π*R/(c-Rω) (1b) .
La differenza di tempo Δt = 2π*R2ω/(c2-R2ω2) ≈ 2π*R2ω/c2) (2) [1] mentre la velocità di rotazione del disco rispetto al Sistema Luce ω = Δt c2/ (2π*R2) (3) .
Occorre evidenziare che in tale esperimento abbiamo considerato la velocità dei 2 raggi di luce indipendente dal moto della sorgente-disco. Il suddetto esperimento comporta un solo SRI: il disco, per cui non possono essere applicate le TL ossia la Relatività. Si ritiene che l’esperimento possa essere descritto come un banale fenomeno di fisica classica. La differenza di tempo dell’effetto Sagnac dimostra che la velocità della luce è diversa nelle due direzioni, in contrasto con il 2° postulato che ipotizza la velocità della luce costante in tutte le direzioni. I relativisti tuttavia obiettano che il sistema disco in rotazione non costituisca un sistema di riferimento inerziale (SRI) e che l’esperimento suddetto possa essere spiegato con la RS o la RG (spiegazioni che risultano non prive di contraddizioni) [2].
[1] L’effetto sagnac – Corsi di Laurea in Fisica pag. 19
[2] L’effetto sagnac – Corsi di Laurea in Fisica Conclusioni e discussioni pag. 57 “… numerosi sono i problemi che nascono quando si cerca di inquadrare l’effetto, sia nell’ambito della teoria della relatività generale che ristretta. …. abbiamo anche osservato che il corretto risultato sperimentale si ottiene solo e soltanto mediante una scelta “fortunata” dei sistemi di riferimento, cosa che contraddice la stessa teoria della relatività. “
4.2.1 Effetto Sagnac e rotazione assoluta. L’effetto Sagnac ha applicazioni pratiche nel giroscopio laser per determinare la rotazione di un velivolo (aereo, nave, …) nello spazio. L’utilizzo di 3 giroscopi nei 3 assi ortogonali permette di individuare la rotazione nello spazio della navicella. L’effetto Sagnac, inoltre, viene utilizzato per correggere la sincronizzazione degli orologi dei GPS. Le onde radio che si scambiano i satelliti quando viaggiano in senso opposto, a causa della rotazione terrestre, devono tener conto dell’effetto Sagnac per sincronizzare gli orologi.
Consideriamo due sistemi di riferimento dotati di giroscopi laser (dischi di Sagnac). I due sistemi, indipendentemente fra loro e senza alcun riferimento con l’esterno, sono in grado di determinare la loro rotazione assoluta facendo riferimento entrambi ad un unico sistema fisso (che si ritiene essere il Sistema Luce).
4.2.2 Effetto Sagnac e velocità assoluta Consideriamo un disco di Sagnac di raggio R molto grande e una piccola asta L di centro B ed estremi AC solidale e tangente al disco (vedi figura in basso). Con una velocità di rotazione ω molto piccola, per un piccolo intervallo di tempo dt, il moto dell’asta può approssimarsi ad un moto rettilineo uniforme con velocità v = ω*R. Cioè l’asta può approssimarsi ad un SRI. Ricordando i tempi impiegati dai 2 raggi nel disco: t1 = π*R/(c+Rω) e t2 = π*R/(c-Rω), i tempi impiegati dai 2 raggi per arrivare agli estremi A e B dell’asta saranno: tA = L/(c+v) e tc =L/(c-v) [1] , mentre la differenza risulta: ΔtAC = 2Lv/(c2 –v2) ≈ 2L*v/c2 (3), da cui è possibile ricavare la velocità dell’asta: v ≈ c2 *ΔtAC/2L[2] (4).
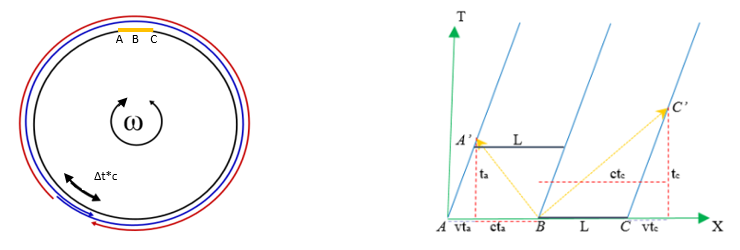 ΔtS = 2πR2ω/(c-Rω) – 2πR/(c+Rω) = 2πR2ω/(c2– (Rω)2) Δt = tC – tA = L/(c-v) – L/(c+v)) = 2*v* L/(c²-v²)
ΔtS = 2πR2ω/(c-Rω) – 2πR/(c+Rω) = 2πR2ω/(c2– (Rω)2) Δt = tC – tA = L/(c-v) – L/(c+v)) = 2*v* L/(c²-v²)
Un disco di Sagnac molto grande e una velocità di rotazione molto piccola permetterebbe di determinare la velocità v del sistema rispetto alla luce. In natura la Terra in rotazione può considerarsi un grande disco di Sagnac. in tal caso, poiché la rotazione avviene attorno ai poli, l’asta AC dovrà essere disposta lungo una parallela. [1]
[1] Per misurare i tempi di arrivo dei 2 raggi in A e C si potrebbero sincronizzare due orologi in B e trasportarli in A e C con la stessa velocità così da subire entrambi una uguale dilatazione temporale. La differenza temporale non dipenderà così dall’orologio in B, ma da 2 orologi che dopo la sincronizzazione subiscono uguali spostamenti con la stessa velocità ma direzioni opposte.
[2] Nel caso in cui la velocità v è relativistica occorre determinare la contrazione dell’asta. In tal caso in prima approssimazione poniamo L senza contrazione L(0). In seconda approssimazione nota v ricaviamo la lunghezza L contratta L(v) . Per iterazioni successive ricaviamo quindi la velocità: v ≈ c2 *ΔtA /2Lγ mentre i tempi diventano: tA = Lγ/(c+v) e tC =Lγ/(c-v) da cui si può ricavare: tA/tC =(c-v)/(c+v).
Velocità e rotazioni assolute. Sistemi di riferimento inerziali dotati di strumenti di Sagnac lineari (molto grandi), indipendentemente l’uno dall’altro, senza alcun riferimento con l’esterno, sarebbero in grado di determinare tramite la 4.2.2 la velocità di traslazione v ≈ ΔtAC c2 /2L. Con 3 giroscopi laser e 3 strumenti Sagnac lineari sarebbe possibile determinare la rotazione e la velocità della navicella rispetto al Sistema Luce.
4.3. Aberrazione cinematica
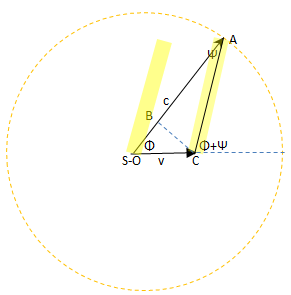
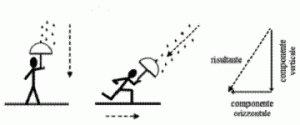
Il fenomeno dell’aberrazione si verifica sia con la pioggia che con la luce ma è più evidente con la pioggia. Se, ad esempio, da fermi la pioggia cade verticalmente con una velocità c , muovendosi con una velocità v le gocce ci colpiscono con una inclinazione (angolo di aberrazione) Ψ ≈ v/c e con una velocità r = c*(1+v²/c²)^½. In generale noto l’angolo Φ compreso tra le velocità c e v è possibile ricavare la velocità risultante r. 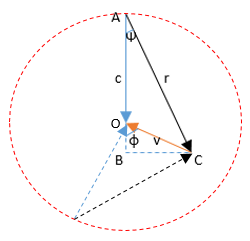 A tale scopo si può fare variare l’angolo Φ facendo ruotare la velocità c attorno ad O. Si ottiene così un cerchio di centro O e raggio c che chiamiamo cerchio di aberrazione (vedi figura). Da esso si può ricavare l’angolo Ψ e la velocità r in funzione di Φ.
A tale scopo si può fare variare l’angolo Φ facendo ruotare la velocità c attorno ad O. Si ottiene così un cerchio di centro O e raggio c che chiamiamo cerchio di aberrazione (vedi figura). Da esso si può ricavare l’angolo Ψ e la velocità r in funzione di Φ.
tanΨ = BC/AC = v*senΦ/(c+v *cosΦ) (1) |r| = (c+v *cosΦ)2+ (v*senΦ)2)1/2 (2)
Qualora si potesse viaggiare a una velocità paragonabile a quella della luce, i raggi di luce ci arriverebbero tanto più inclinati e fitti quanto più alta sarebbe la nostra velocità. Questo effetto viene definito aberrazione stellare. Per velocità relativistiche dell’osservatore occorre tenere conto della contrazione relativistica.
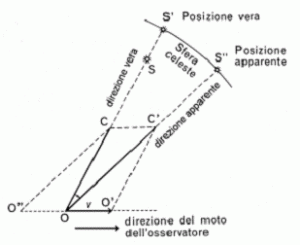
4.3.1 Aberrazione e velocità assoluta. Supponiamo di non conoscere la propria velocità e di trovarci nell’istante iniziale nel punto O. Se da tale punto si emettono dei lampi di luce in tutte le direzioni dopo il tempo unitario essi si troveranno sulla circonferenza di centro O e raggio c mentre noi ci troveremo in un punto C sconosciuto. Se osserviamo la suddetta circonferenza si rileva però che è sufficiente conoscere 2 angoli Ψ per conoscere tale punto C, in quanto intersezioni delle 2 direzioni r. Per il calcolo della velocità v, si può posizionare il braccio OA lungo una direzione e fare partire da O un lampo di luce nella direzione OA. Poiché il braccio OA è in moto il lampo di luce percorrerà una direzione che formerà con la direzione OA un angolo di aberrazione Ψ che possiamo misurare e con esso la direzione di r. Posizionando il braccio in un’altra direzione OA’ otteniamo un altro angolo Ψ’ e un’altra direzione r’. L’intersezione delle 2 direzioni trovate da il punto C, quindi la nostra velocità v= OC. [1]
[1] Tale fenomeno di aberrazione corrisponde all’aberrazione stellare dove il cannocchiale deve essere inclinato (secondo l’angolo di aberrazione) per far arrivare i raggi di luce all’oculare del cannocchiale , qui invece i raggi effettuano il percorso inverso partono da O (corrispondente all’oculare)2.
4.3.2. Ellisse di aberrazione relativistica. Poiché nei sistemi in moto con velocità v si ha una dilatazione 1/γ del tempo il suddetto cerchio di aberrazione si dilata lungo la direzione del moto e assume la forma di una ellisse (vedi ellisse di aberrazione del paragrafo 3.2), quindi dalla (1) si ha: tanΨ’ = v*senΦ /γ*(c+v *cosΦ). Si fa rilevare che a meno della contrazione 1/γ per l’osservatore in moto le velocità radiali c e la velocità v si sommano come per l’aberrazione cinematica. Ossia per l’osservatore in moto la luce può assumere velocità maggiori o minori di c. Inoltre l’angolo di aberrazione non dipende dal moto delle stelle (proprietà 1) ma solo dalla velocità dell’osservatore in quanto la velocità c della luce emessa dalle stelle è costante. L’ellisse di aberrazione si ritiene una prova che esiste un sistema di riferimento privilegiato per il quale l’ellisse di aberrazione è un cerchio. Per il “Sistema Luce” non si hanno fenomeni di aberrazione.
Per spiegare l’aberrazione relativistica possiamo utilizzare il filmato sfere e aberrazione. In esso la condizione data è che i percorsi di andata e ritorno dei raggi di luce dal centro alle pareti siano uguali. Si osserva che per l’osservatore solidale con il sistema luce i punti di contatto tra i raggi di luce (che partono dal centro) e le pareti della sfera (contratta lungo la direzione del moto) costituiscono l’ellisse di aberrazione. Si fa notare che nella sfera ferma l’osservatore al centro non vede i raggi deviati  (aberrati) in quanto l’ellisse di aberrazione è una circonferenza.
(aberrati) in quanto l’ellisse di aberrazione è una circonferenza.
Nella sfera in moto (in rosso e contratta lungo la direzione del moto) i raggi di luce partono dall’origine O (0;0), toccano le pareti della suddetta sfera in istanti diversi e arrivano al centro O’ contemporaneamente dopo un tempo 2t’ = 2t*γ con γ =1/(1-v2/c2)1/2. In tale intervallo di tempo il centro O si sposta in O’ di OO’= 2v*t’ = 2vt*γ, mentre i raggi percorrono nel tempo 2t’ = 2t*γ tutti lo stesso spazio OPO’ = 2ct*γ. I punti di contatto Pi tra i raggi e la sfera in moto descrivono l‘ellisse blu avente fuochi O e O’, semiasse maggiore RS = ct*γ e semiasse minore r = ct. Posto PS = ct =1:
- OS = OO’/2 = vt*γ = β*γ,
- RO = RS-OS = (c–v)t*γ = ct*(1-β)*γ = (1-β) *γ,
- RO’= RS+OS = (c+v)t*γ = ct*(1+β)*γ= (1+β)*γ.
4.3.3 Effetto Sagnac e Aberrazione – stesso fenomeno. Se dividiamo membro a membro le distanze: RO/RO’ = (c-v)/(c+v) e dividiamo i tempi impiegati dai raggi per l’asta L in moto: tA/tC =(c-v)/(c+v) si ricava la relazione RO’/RO = tA/tC =c*tA/c*tC , ossia i bracci dell’ellisse RO’ ed RO sono proporzionali alle distanze AB e BC dell’asta L percorse dai raggi. Cioè l’elisse di aberrazione, l’asta in moto e il disco di Sagnac in rotazione sono fenomeno costituiti da un sistema in moto e raggi di luce che effettuano percorsi unidirezionali. Per essi si ha la somma delle velocità c+v e c-v (che contraddicono il 2° postulato). Si osserva che i raggi:
- Nell’asta in moto e nel disco in rotazione partono dal sistema in moto (il centro B dell’asta);
- Nell’ellisse di aberrazione partono dalle stelle e arrivano al sistema (osservatore in moto).
NOTA: In Appunti di Relatività Speciale -Roberto Casalbuoni -Dipartimento di Fisica dell’Università di Firenze a.a. 2004-2005 sul sito: http://theory.fi.infn.it/casalbuoni/lavori/relativita.pdf a pag. 31 per spiegare l’aberrazione relativistica si fa ricorso al riferimento assoluto. Ciò è palesemente in contraddizione con la RS che non ammette alcun riferimento particolare.
4.4 L’effetto Doppler. Mentre l’aberrazione costituisce la composizione della velocità c (costante) della luce e della velocità v del sistema. L’effetto Doppler (blueshift e redshift), oltre alla composizione delle 2 velocità “c” e “v” (aberrazione), tiene conto della variazione della distanza tra sorgente e osservatore, la quale crea un cambio di frequenza. Le formule dell’effetto Doppler risultano pertanto uguali a quelle dell’aberrazione, se alla velocità assoluta v del sistema si sostituisce la velocità relativa v’ tra osservatore e sorgente (stelle). Infatti se consideriamo le distanze/velocità RO ed RO’ dell’ellisse di aberrazione ponendo β’ = v’/c gli effetti Doppler relativistici in avvicinamento e in allontanamento valgono:
- RO’ = (1+β’)*γ = (1+β’)/ (1-β’2)1/2 = ((1+β’)2/ (1-β’2))1/2 = ((1+β’)/ (1-β’))1/2
- RO = (1-β’)*γ = (1-β’)/ (1-β’2)1/2 = ((1-β’)2/ (1-β’2))1/2 = ((1-β’)/ (1+β’))1/2
Riassumendo:
- La RS non è idonea a spiegare i fenomeni con 1 solo SR (sistema di riferimento);
- Considerando le 2 proprietà della luce è possibile definire il Sistema Luce.
- Il Sistema Luce permette lo studio dei fenomeni con 1 solo SR;
- Con fenomeni aventi 1 solo SRI e luce bidirezionale è possibile spiegare la reale deformazione dello spazio e del tempo proprio del sistema;
- Con fenomeni aventi 1 solo SRI e luce unidirezionale è possibile trovare i moti di traslazione e rotazione assoluti (reali) dei sistemi.



 sono egualmente, anche se limitatamente, validi. E’ la filosofia del relativismo e del soggettivismo che si afferma in fisica per le tipiche constatazioni degli osservatori in moto. – Ehrenfest sentì molto acutamente l’esistenza di questo genere di problemi. La teoria di relatività speciale basata sulla negazione dell’etere richiede la completa equivalenza degli osservatori in moto relativo uniforme, perché non c’è ragione che siano inequivalenti, dato che si muovono rispetto al nulla. Tuttavia se si adotta il principio d’equivalenza che Einstein formulò nel 1916 e su cui basò la teoria di relatività generale, si conclude che l’inerzia ha la sua origine negli effetti gravitazionali delle masse lontane, effetti mediati da campi fisici presenti nello spazio vuoto. Ma la parola etere e la parola campo indicano all’incirca la stessa cosa, un vuoto dotato di proprietà fisiche. Questa contraddizione angustiava Ehrenfest che nel 1919 scrisse ad Einstein: “Ora non si può più dire che si muovono rispetto al nulla, perché si muovono rispetto a un enorme qualcosa! … Einstein, il mio stomaco disturbato odia la tua teoria – quasi odia anche te! Come posso educare i miei studenti? E cosa posso rispondere ai filosofi?!!”
sono egualmente, anche se limitatamente, validi. E’ la filosofia del relativismo e del soggettivismo che si afferma in fisica per le tipiche constatazioni degli osservatori in moto. – Ehrenfest sentì molto acutamente l’esistenza di questo genere di problemi. La teoria di relatività speciale basata sulla negazione dell’etere richiede la completa equivalenza degli osservatori in moto relativo uniforme, perché non c’è ragione che siano inequivalenti, dato che si muovono rispetto al nulla. Tuttavia se si adotta il principio d’equivalenza che Einstein formulò nel 1916 e su cui basò la teoria di relatività generale, si conclude che l’inerzia ha la sua origine negli effetti gravitazionali delle masse lontane, effetti mediati da campi fisici presenti nello spazio vuoto. Ma la parola etere e la parola campo indicano all’incirca la stessa cosa, un vuoto dotato di proprietà fisiche. Questa contraddizione angustiava Ehrenfest che nel 1919 scrisse ad Einstein: “Ora non si può più dire che si muovono rispetto al nulla, perché si muovono rispetto a un enorme qualcosa! … Einstein, il mio stomaco disturbato odia la tua teoria – quasi odia anche te! Come posso educare i miei studenti? E cosa posso rispondere ai filosofi?!!”
