La Relatività senza paradossi
Premessa:
Le costanti elettrica ε e magnetica μ sono state definite per descrivere i campi statici (in assenza di moto), prodotti da una carica elettrica e da un magnete. Con cariche o magneti in moto Maxwell ha scoperto che l’onda elettromagnetica si propaga nello spazio con velocità costante (velocità della luce c) dipendente proprio da tali costanti ε e μ. 
(1)
Con gli esperimenti di Michelson e Morley, finalizzati alla ricerca dell’etere, si è scoperto la costanza/invarianza della velocità della luce in percorsi di andata e ritorno, per qualunque velocità del sistema (interferometro). Per poter spiegare questo strano fenomeno si è dovuto ipotizzare che il tempo e lo spazio fossero deformabili con la velocità del sistema. Le Trasformazioni di Lorentz (sulle quale si fonda La Teoria della Relatività) sono state ricavate ipotizzando altresì (2° postulato della RS) la costanza della velocità della luce c lungo una sola direzione per tutti i sistemi di riferimento (ossia per qualsiasi velocità del sistema). Da tale ipotesi deriva il paradosso matematico c-v = c = c+v. Tale equazione non risulta valida in quanto la velocità c ha un valore non infinito (300.000 km/s). Questa equazione, d’altra parte, non è mai stata dimostrata da nessun esperimento.
Gli esperimenti di Michelson e Morley dimostrano infatti : “La costanza della velocità della luce nel vuoto in un percorso di andata e ritorno in tutti i sistemi di riferimento“. Tale costanza della velocità della luce ci permette di ricavare una deformazione dello spazio – tempo in funzione della velocità v che solo “nella forma” risulta uguale alla deformazione di Lorentz. Nell’esempio di seguito tale invarianza ci permette di definire la deformazione dello spazio e del tempo, considerando la deformazione di una sfera in moto: “una sfera è realmente tale (qualunque sia la sua velocità) se i raggi nel percorso dal centro alle pareti e ritorno impiegano lo stesso tempo”.
Consideriamo, quindi, due sfere di raggio unitario (rappresentanti 2 sistemi di riferimento), la prima ferma rispetto ai raggi di luce l’altra in moto con velocità v=c/2. Per quanto detto, le 2 sfere sono effettivamente sfere se per ciascuna sfera i raggi di luce, partendo dal loro centri in direzioni diverse, dopo essere stati riflessi dalle pareti di tali sfere, ritornano ai centro contemporaneamente.
Si osserva dal filmato che: Nella sfera ferma i raggi di luce partono dal centro e ritornano al centro contemporaneamente dopo un tempo t= 1; Nella sfera in moto, invece, i raggi percorrono una traiettoria obliqua (per l’osservatore esterno) in un tempo t’ maggiore di t (dilatazione del tempo). Nel sistema in moto la luce impiega più tempo ossia rallenta. Inoltre nella direzione del moto, poiché la luce deve impiegare lo stesso tempo in tutte le direzioni, si ha una contrazione dello spazio. .
Il filmato spiega che, con la condizione di invarianza della velocità della luce in un percorso bidirezionale, in che modo il tempo si dilata e lo spazio si contrae. Inoltre da essa si rileva che i raggi arrivano alle pareti in tempi diversi, per cui eventi simultanei per l’osservatore esterno non lo sono per l’altro osservatore. Per la Relatività Speciale, l’osservatore solidale alla sfera in moto ritiene ferma la sua sfera e in moto l’altra, inoltre vede partire i raggi di luce dal centro della sua sfera e li vede ritornare tutti nello stesso istante.
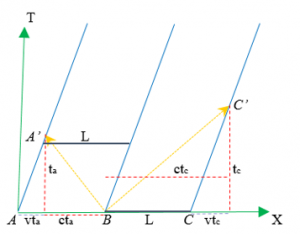
Calcoliamo la  dilatazione del tempo t’. Nella sfera in moto il raggio di luce che si muove in direzione y per l’osservatore S’, per l’osservatore S esterno si muove lungo la diagonale. Il tempo lungo la diagonale t’ è maggiore del tempo t lungo la verticale. La sfera infatti durante il tempo t’ si sposta di v*t’ per cui possiamo considerare il triangolo rettangolo avente come cateti: il raggio lungo la verticale: r = c*t e lo spostamento: dx = v*t’, e come ipotenusa la diagonale c*t’. Dal teorema di Pitagora: c2*t2=c2*t’2-v2*t’2 quindi la dilatazione: t’ = t/(1- v2/ c2)1/2 posto (1- v2/ c2)1/2 = γ si ha t’ = t / γ (2)
dilatazione del tempo t’. Nella sfera in moto il raggio di luce che si muove in direzione y per l’osservatore S’, per l’osservatore S esterno si muove lungo la diagonale. Il tempo lungo la diagonale t’ è maggiore del tempo t lungo la verticale. La sfera infatti durante il tempo t’ si sposta di v*t’ per cui possiamo considerare il triangolo rettangolo avente come cateti: il raggio lungo la verticale: r = c*t e lo spostamento: dx = v*t’, e come ipotenusa la diagonale c*t’. Dal teorema di Pitagora: c2*t2=c2*t’2-v2*t’2 quindi la dilatazione: t’ = t/(1- v2/ c2)1/2 posto (1- v2/ c2)1/2 = γ si ha t’ = t / γ (2)
Dalla relazione c2 * t2 = c2 * t’2 – v2 * t’2 si osserva che la grandezza spazio tempo d2 = c2 * t2 non varia con la velocità v, essa è cioè un’invariante e può essere scritta: d2 = c2 * t’2 – dx’2 = cost.
Calcoliamo la contrazione dello spazio x’. Consideriamo il raggio di luce nella direzione x. Se la parete va incontro al raggio esso impiega un tempo t’ = r/(c+v), mentre se la parete si allontana il raggio impiega un tempo t” = r/(c-v) . Il tempo totale di andata e ritorno risulta: t’+t’’ = r/(c+v)+r/(c-v) = r(c+v +c-v) / (c2-v2) = 2rc/(c2-v2) = 2r/c/(1- v2/c2) → tx = r/c/(1- v2/c2) = t /(1- v2/c2) → tx = t / γ2 tale tempo tx risulta più lungo del tempo dilatato t’ = tx / γ di un fattore 1/γ. Poiché deve essere verificata la condizione della costanza della velocità della luce in tutte le direzioni, tale maggior tempo viene compensato (dalla natura) con la contrazione γ dello spazio lungo la direzione del moto, ossia Lx = L* γ (3).
In definitiva: si ha una contrazione dello spazio nella direzione del moto in quanto la velocità c della luce, nel suo percorso di andata e ritorno, rimane costante in tutte le direzioni.
Ipotizzando che la materia (con le sue particelle) interagisca alla velocità della luce, si possono ritenere reali la dilatazione del tempo e la contrazione dello spazio.
ll tempo e lo spazio. Con la suddetta condizione si può dedurre che la materia (con le sue particelle) interagisca alla velocità della luce nelle due direzioni (di andata e ritorno). Lo scorrere del tempo per le particelle può identificarsi come la velocità di interazione (mediante campi potenziali) tra essi. Tale interazione avviene mediante i campi (di forza) che viaggiano alla velocità della luce in uno spazio a 3 dimensioni. Con tale condizione, inoltre, lo spazio-tempo a 4 dimensioni non esiste. D’altra parte le forze dovrebbero avere una distribuzione nello spazio secondo una legge 1/r³, che contrasterebbe con l’equazione di continuità dei campi. Vedi a proposito l’articolo: Vuoto, energia e materia. In definitiva il corpo con la sua velocità modifica il proprio tempo e la propria forma per mezzo della luce, mentre il campo prodotto dal corpo modifica/rallenta la velocità della luce.
Vedi La luce come Sistema di Riferimento assoluto.