Aberrazione cinematica. 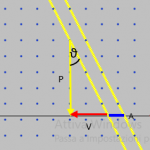 Viene definita aberrazione cinematica la diversa direzione della pioggia, luce ecc. percepita dall’osservatore in moto rispetto all’osservatore fermo. Ad esempio quando piove in assenza di vento e stiamo fermi è evidente che le gocce che ci bagnano stanno lungo la nostra verticale. Se la pioggia cade con velocità p e l’osservatore è in moto con velocità v, questi, vede cadere la pioggia con una velocità complessiva r = p -v, mentre le gocce che ci colpiscono ogni secondo (Δt = 1) stanno su una colonna avente inclinazione v/p, rispetto alla verticale, e lunghezza L= 1*(p2+v2)1/2 metri. Per tale motivo ad esempio quando si viaggia in auto la quantità di pioggia sul parabrezza aumenta mentre su lunotto diminuisce.
Viene definita aberrazione cinematica la diversa direzione della pioggia, luce ecc. percepita dall’osservatore in moto rispetto all’osservatore fermo. Ad esempio quando piove in assenza di vento e stiamo fermi è evidente che le gocce che ci bagnano stanno lungo la nostra verticale. Se la pioggia cade con velocità p e l’osservatore è in moto con velocità v, questi, vede cadere la pioggia con una velocità complessiva r = p -v, mentre le gocce che ci colpiscono ogni secondo (Δt = 1) stanno su una colonna avente inclinazione v/p, rispetto alla verticale, e lunghezza L= 1*(p2+v2)1/2 metri. Per tale motivo ad esempio quando si viaggia in auto la quantità di pioggia sul parabrezza aumenta mentre su lunotto diminuisce.
Posto p= c e indicato con Φ l’angolo tra le velocità c e v, il vettore risultante r = c-v forma con c l’angolo di aberrazione Ψ con: 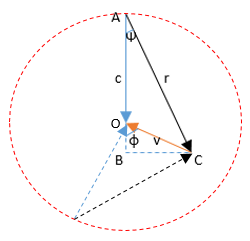 tan(Ψ) = BC/AB = v*sen(Φ)/(c+v *cos(Φ)) (1) mentre il modulo r = ((c+v *cos(Φ))2+ (v*sen(Φ))2)1/2 (2)
tan(Ψ) = BC/AB = v*sen(Φ)/(c+v *cos(Φ)) (1) mentre il modulo r = ((c+v *cos(Φ))2+ (v*sen(Φ))2)1/2 (2)
Se ruotiamo la velocità c attorno ad O e lasciamo invariata la velocità v, si ottiene un cerchio di centro O e raggio c, in cui possiamo misurare, per ogni angolo Φ compreso tra i vettori c e v, l’angolo di aberrazione Ψ e il modulo di r. Dalla (1) si rileva che per Φ =90° l’aberrazione tan(Ψ) = v/c è massima (c e v sono ortogonali) mentre per Φ =90° l’aberrazione Ψ =0 (c e v hanno la stessa direzione). Dalla (2) si rileva che il vettore r converge sempre nel punto C distante v da O e varia da un massimo di r = c+v ad un minimo di r = c-v.
Aberrazione stellare. Si chiama aberrazione stellare la direzione apparente delle stelle dovuta alla velocità relativa Terra-Luce. Infatti il moto v della Terra attorno al Sole si compone con la velocità c della luce delle stelle. L’aberrazione è massima per le stelle poste nella direzione ortogonale al piano dell’eclittica, ossia ortogonale alla velocità v della Terra, mentre è nulla per le stelle poste sull’eclittica (ossia parallela alla velocità v della Terra). Se si osserva la posizione della stella per un anno essa descrive una ellisse più o meno schiacciata dipendente dalla sua posizione rispetto al piano dell’eclittica. Infatti, poiché la Terra compie una rotazione attorno al Sole, la velocità v della Terra compie una rotazione (ellisse), così come la risultante r = c-v della velocità c della luce e v della Terra.
In aberrazione stellare sono rappresentati dei fotoni con direzione verticale mentre il cannocchiale e in moto orizzontale. I fotoni osservabili dal cannocchiale (ossia che lo attraversano) in moto con velocità v, hanno un angolo di inclinazione/aberrazione v/c. Quando si è in moto, come per le gocce di pioggia, il numero di fotoni che ci arriva dipende dalla direzione del nostro movimento rispetto alla direzione dei fotoni ed è proporzionale alla risultante r dei vettori velocità r = c±v . Tale relazione (che descrive un fenomeno della natura), a parere dello scrivente, contraddice il 2° postulato della TdR.
Aberrazione relativistica – Ellisse di aberrazione. Se si osserva la volta celeste per trovare l’aberrazione di ogni stella possiamo considerare il cerchio sopra descritto, considerando v la velocità della Terra e la velocità c della luce delle stelle proveniente da tutte le direzioni. Tali direzioni a causa dell’aberrazione vengono percepite con direzione r e confluiscono nel punto C decentrato della velocità v. Nel caso in cui la velocità v fosse elevata per calcolare l’aberrazione occorre tenere conto della reale contrazione 1/γ (<1) del corpo lungo la direzione del moto. Per l’osservatore in moto: l’ellisse rossa corrisponde al cerchio mentre il cerchio suddetto di raggio c corrisponde all’ellisse blu di assi c e c*γ .
Dalla (1) si ricava pertanto la relazione: tan(Ψ) = v*sen(φ)/ (c+v*cos(φ))*γ (1a). Dalla quale si rileva che per Φ =90° tan(Ψ) = v/(γc) è massimo (c e v sono ortogonali) mentre per Φ =90° l’aberrazione Ψ =0.
Un altro modo per ricavare l’aberrazione relativistica utilizza l’esempio delle sfere in moto. Abbiamo visto che la sfera in moto subisce una contrazione, pertanto per l’osservatore in moto la sfera (dei raggi) di luce viene vista come una ellisse (di aberrazione) allungata nella direzione del moto. Dalla sfere in moto si osserva che i punti di contatto tra i raggi (che partono dal centro) e le pareti della sfera in moto compongono l’ellisse di aberrazione cercata. L’osservatore solidale con 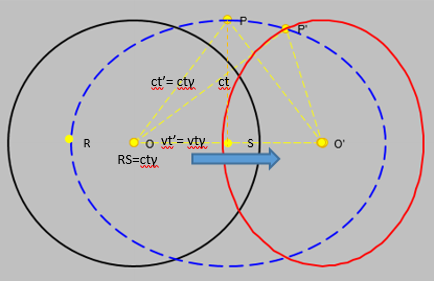 la sfera ferma (nera) non vede nessuna deviazione dei raggi. L’osservatore solidale con la sfera in moto (rossa e contratta lungo la direzione del moto) vede i raggi di luce deviati. Infatti i raggi partono dall’origine O (0;0), toccano le pareti della suddetta sfera in istanti diversi e arrivano al centro O’ contemporaneamente dopo un tempo 2t’ = 2t*γ (con γ =1/(1-v2/c2)1/2). In tale intervallo di tempo il centro O si sposta in O’ di OO’= 2v*t’ = 2vt*γ, mentre i raggi nel tempo 2t’ = 2t*γ percorrono tutti lo stesso spazio OPO’ = 2ct*γ. Poiché i raggi partono tutti da O e arrivano in O’ nello stesso istante, hanno lunghezza uguale, i punti di contatto raggi-sfera (rossa) Pi descrivono l‘ellisse blu di fuochi O e O’, semiasse maggiore RS = ct*γ, semiasse minore r = ct (poniamo r= ct =1).
la sfera ferma (nera) non vede nessuna deviazione dei raggi. L’osservatore solidale con la sfera in moto (rossa e contratta lungo la direzione del moto) vede i raggi di luce deviati. Infatti i raggi partono dall’origine O (0;0), toccano le pareti della suddetta sfera in istanti diversi e arrivano al centro O’ contemporaneamente dopo un tempo 2t’ = 2t*γ (con γ =1/(1-v2/c2)1/2). In tale intervallo di tempo il centro O si sposta in O’ di OO’= 2v*t’ = 2vt*γ, mentre i raggi nel tempo 2t’ = 2t*γ percorrono tutti lo stesso spazio OPO’ = 2ct*γ. Poiché i raggi partono tutti da O e arrivano in O’ nello stesso istante, hanno lunghezza uguale, i punti di contatto raggi-sfera (rossa) Pi descrivono l‘ellisse blu di fuochi O e O’, semiasse maggiore RS = ct*γ, semiasse minore r = ct (poniamo r= ct =1).
Si ha: OO’= 2v*t’ = 2vt*γ , PS = ct = 1 , OS = OO’/2 = vt*γ, RS = ct*γ;
RO = RS-OS = ct*γ – vt*γ = ct*(1-β) *γ RO = (1-β) *γ = (1-v/c)* γ,
OS = RS- RO = γ – (1-β) *γ = β*γ , RO’ = RO + OO’ = (1-β) *γ + 2β*γ = (1+v/c)*γ
Si fa osservare che tutti i raggi di luce, che partono dalle pareti della sfera in moto, arrivano nel fuoco O’ contemporaneamente. Cioè l’osservatore in moto v vede arrivare i raggi di luce, provenienti dalla sfera (celeste) nel punto O’, deviati e deformati secondo tale ellisse (di aberrazione).
L’ellisse di aberrazione si ricava quindi dilatando la sfera nella direzione del moto di un fattore γ per cui il punto C , in cui convergono i raggi, dista v*γ da O. Si evidenzia che nell’aberrazione relativistica le velocità radiali c e la velocità v si sommano e si sottraggono come per l’aberrazione cinematica.
L’aberrazione della luce, a mio parere, contraddice il 2° principio della relatività secondo cui la velocità della luce è costante in tutti i sistemi di riferimento (cioè una persona sia ferma sia in moto percepisce la stessa velocità della luce). L’aberrazione luminosa infatti fa percepire la luce in una direzione diversa dalla direzione effettiva a causa del movimento v dell’osservatore. La direzione risultante r = c-v (differenza vettoriale della velocità luce c e della velocità dell’osservatore v), costituisce la velocità vettoriale della luce percepita dall’osservatore.
Effetto Doppler relativistico. L’effetto Doppler (blueshift e redshift), che è l’aumento/diminuzione della frequenza a causa del moto relativo tra sorgente e osservatore, ha la stessa formula dell’aberrazione a meno di sostituire la velocità v dell’osservatore con la velocità relativa tra osservatore e sorgente (stelle). Pertanto l’ellisse di aberrazione non è valida per l’effetto Doppler.
L’effetto Doppler relativistico in avvicinamento e in allontanamento, ricordando che β =v’/c e che v’ è la velocità Osservatore-Stella, vale :
RO’ = (1+β)*γ = (1+β)/ (1-β2)1/2;= ((1+β)2/ (1-β2))1/2 = ((1+β)/ (1-β))1/2
RO = (1-β)*γ = (1-β)/ (1-β2)1/2;= ((1-β)2/ (1-β2))1/2 = ((1-β)/ (1+β))1/2
Sistema Luce e nuovo significato delle grandezze relativistiche.
Se si osservano le equazioni (1) e (1a) si nota che in entrambi l’aberrazione si ottiene dalla somma vettoriale della velocità v e della velocità c della luce proveniente da tutte le direzioni. In entrambi i casi la risultante r di c e di v non rimane costante, ciò, in disaccordo con il 2° postulato della Relatività che prevede la costanza della velocità della luce c in tutte le direzioni. D’altra parte si è visto che, per ottenere l’ellisse di aberrazione relativistica, non si è applicato il 2° postulato della relatività, ma la condizione della costanza della velocità della luce in un percorso di andata e ritorno.
L’ellisse di aberrazione dimostra cioè che i sistemi di riferimento non sono tutti uguali per cui il 2° postulato è errato. Infatti, se l’ellisse di aberrazione è una circonferenza la velocità v dell’osservatore deve essere nulla per tutti i raggi di luce, qualunque sia la loro direzioni. Tale sistema può considerarsi un sistema di riferimento privilegiato, a differenza di quanto prevede la Relatività. Poiché per tale sistema non si hanno fenomeni di aberrazione della luce esso si potrebbe chiamasi “Sistema Luce”.
Definito in tal modo il “Sistema Luce”, facendo riferimento ad esso possiamo definire la velocità (assoluta) di tutti gli altri sistemi. Definire, in maniera concreta (e non come vengono definite dalla Relatività), l’energia a riposo e l’energia relativistica riferita al Sistema Luce.
Disgressioni sul significato temporale e spaziale dell’aberrazione.
Poiché l‘energia (della luce) può essere definita come il numero n di quanti h nell’unità di tempo t: E= h*v = h*n/t (in quanto v= n/t) e considerato che il tempo si dilata con la velocità: t’ = t*γ (per cui l’ellisse si dilata), si può supporre che l’energia relativistica: E’ =n*h/t’ aumenti in quanto in un intervallo di tempo più lungo scorra più luce. Ossia, fissato lo spazio, maggiore è il tempo t’ maggiore è il numero di quanti (fotoni) che attraversano tale spazio.
Poiché la quantità di moto della luce può essere definita come il numero n di quanti h nell’unità di spazio L: P = h*n/L (in quanto la λ= L/n) e considerato che lo spazio si contrae con la velocità L’=L/γ si può supporre che la quantità di moto relativistica: P’ = h*n/L’ diminuisca in quanto, in un intervallo di spazio più corto, sia presente meno luce. Ossia fissato il tempo, minore è lo spazio L’ minore è il numero di quanti (fotoni) contenuti in tale spazio.
Non sembra superfluo, altresì, supporre dei legami tra onde stazionarie in un atomo e i percorsi di andata e ritorno delle onde di luce. …
 Chi è costui nella foto? Fino a pochi mesi fa non lo conoscevo nemmeno io è Oliver Heaviside. Rispetto a tanti altri “geni” della fisica ritengo che egli sia uno tra i più dimenticati e sconosciuti. Quasi tutti hanno sentito parlare delle equazioni di Maxwell ma pochissimi sanno che esse sono costituite da 20 equazioni con una matematica complicatissima come i quaternioni. Le 4 equazioni che oggi si studiano come Equazioni di Maxwell sono state scritte da questo individuo con un lavoro di pulizia e di semplificazione delle 20 equazione differenziali. Difficilmente le equazioni scritte da Maxwell potevano essere capite e gestite dai fisici.
Chi è costui nella foto? Fino a pochi mesi fa non lo conoscevo nemmeno io è Oliver Heaviside. Rispetto a tanti altri “geni” della fisica ritengo che egli sia uno tra i più dimenticati e sconosciuti. Quasi tutti hanno sentito parlare delle equazioni di Maxwell ma pochissimi sanno che esse sono costituite da 20 equazioni con una matematica complicatissima come i quaternioni. Le 4 equazioni che oggi si studiano come Equazioni di Maxwell sono state scritte da questo individuo con un lavoro di pulizia e di semplificazione delle 20 equazione differenziali. Difficilmente le equazioni scritte da Maxwell potevano essere capite e gestite dai fisici.

