Considerati i punti di una funzione f(x) la trasformata di Legendre g(p) può essere rappresentata come i valori cambiati di segno delle intercette sull’asse y delle rette tangenti (inviluppo) alla funzione (curva) f(x) con pendenze p= f’(x)
g(p)= max( p*x –f(x)) (1)
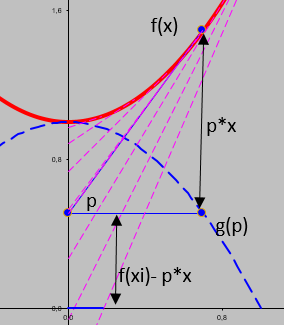In figura la tangente alla f(x)= x2+1 nel punto (0,7; 1,49) ha pendenza p= f’(0,7) = 2*x = 1,4 e intercetta l’asse y nel punto g(p) = f(xi) – p*xi = 1,49- 1,4*0,7 =0,51. Sono riportate, in fuxia, altre tangenti alla f(x) che intercettano l’asse y in altri punti g(p) e in blu d(g(p))tratteggiata la curva g(p) .
La trasformata di Legendre può essere, altresì, definita: Dato un punto f(xs) della curva e considerato il fascio di rette parallele y(k)= p*x +k di pendenza p= f’ (xs), quella che è tangente alla curva deve avere k = f(xs)-p*xs , cioè deve intersecare l’asse y in -g(p). In figura il fascio di rette è: y(k) = p*x – k La retta tangente si ha per k = f(xs)-p*xs= 1,25 – 1*0,5 = 0,75 = g(p).
La trasformata di Legendre è una involuzione cioè se applicata due volte dà il valore originario (ad esempio se si inverte due volte un numero razionale si ottiene il numero di partenza).
Si osserva che se si deriva rispetto alla variabile p la (1): g(p)= x*p -f(x) si ricava x = d(g(p))/d(p) (2) ricordando che p = f’ si può scrivere x = d(g(p))/d(f’) (2a). Si fa osservare dalla (2a) che, con la trasformata g(p) della funzione f(x), nella derivata f’ = df(x)/dx, si inverte la x con la f’ (= p) .
Vediamo di ricavare la g(p) mediante la (1).
Consideriamo f(x) descritta con il monomio: f(x) =α*xn , calcoliamo p = f’(x) → p = α*n*xn-1 il differenziale è: dp = α*(n-1)*n*xn-2*dx → x*dp = α*(n-1)*n*xn-1*dx per la (1) dg(p) = x(p)*dp → dg(p) = α*(n-1)*n*xn-1*dx = d(α*(n-1)* xn) quindi g(p) = α*(n-1)*xn-1*x = α*n*xn-1*x – α*xn = p*x –f. La funzione che verifica la (1) è quindi: g(p) = p*x-f(x).
Esempio: Consideriamo la funzione in figura f(x)= x2 +1 da cui g(p) = p*x- x2 -1 il minimo si ha per g’(p)= p – 2*x = 0 ossia per x(p) = p/2 f(p)= p2/4+1. Se x=0,5 , p(0,5) = 1 , g(0,5) = 1*0,5- 0,52 -1 = – 0,75.
In analisi funzionale, si ricorda che la Lagrangiana esprime l’energia totale del sistema L(qi,t) =T – V (con T E.cinetica e V E.potenziale) mediante le coordinate q(xi,t), l’hamiltoniana H invece esprime l’energia totale del sistema con le derivate q’ delle coordinate lagrangiane, ossia H(qi‘,t). Cioè l’hamiltoniana H costituisce la trasformata di Legendre della lagrangiana L del sistema: p = dL/dq’ se si inverte p con q’ si ha: q = dH/dp’ con la trasformata H = p*q’ – L.