Relatività Generale (ascensore in caduta libera)
Consideriamo un ascensore in caduta libera (sistema non inerziale) . L’osservatore all’interno non rileva alcuna forza, tuttavia, il suo spazio-tempo si deforma.
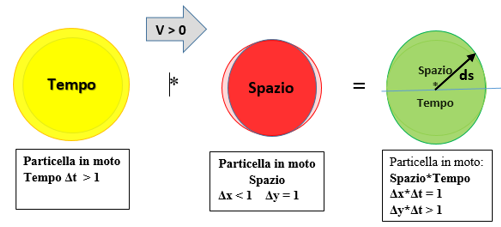
Deformazione del tempo. Consideriamo un sistema di riferimento non inerziale, ad esempio un missile con accelerazione costante. In un diagramma Spazio – Tempo, esso descrive una parabola.
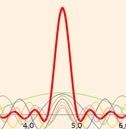
 La velocità (pendenza della parabola) aumenta con il tempo. Rappresentiamo in tale diagramma con due parabole le posizioni, nel tempo, della parete anteriore e posteriore del missile. Su tali pareti poniamo due orologi, che emettono raggi di luce a intervalli regolari, rappresentati in figura da frecce arancioni e blu, di uguale lunghezza÷tempo e di uguale pendenza÷velocità (delle luce). Si nota che: per l’osservatore posto nella parte posteriore del missile l’orologio posto avanti accelera. Infatti la luce di tale orologio arriva sempre più in anticipo : nella figura si nota che man mano le frecce arancione arrivano sulla parabola (parete superiore) sempre più in anticipo; mentre per l’osservatore posto nella parte anteriore l’ orologio posto dietro decelera. Infatti la luce arriva sempre più in ritardo: nella figura le frecce blu ritardano sempre di più per raggiungere la parete anteriore.
La velocità (pendenza della parabola) aumenta con il tempo. Rappresentiamo in tale diagramma con due parabole le posizioni, nel tempo, della parete anteriore e posteriore del missile. Su tali pareti poniamo due orologi, che emettono raggi di luce a intervalli regolari, rappresentati in figura da frecce arancioni e blu, di uguale lunghezza÷tempo e di uguale pendenza÷velocità (delle luce). Si nota che: per l’osservatore posto nella parte posteriore del missile l’orologio posto avanti accelera. Infatti la luce di tale orologio arriva sempre più in anticipo : nella figura si nota che man mano le frecce arancione arrivano sulla parabola (parete superiore) sempre più in anticipo; mentre per l’osservatore posto nella parte anteriore l’ orologio posto dietro decelera. Infatti la luce arriva sempre più in ritardo: nella figura le frecce blu ritardano sempre di più per raggiungere la parete anteriore.

Deformazione dello spazio. Un raggio di luce s entra da un lato dell’ascensore in caduta libera percorrendo una traiettoria rettilinea ( linea rossa ). Per l’osservatore posto all’interno, a causa della sua caduta assieme all’ascensore, la traiettoria del raggio di luce non é una retta ma una curva ( linea gialla ). Lo spazio cioè si deforma .
In tale esperimento si ipotizza valida la relazione: m. inerziale = m. gravitazionale mi = mg (1) La massa inerziale e’ presente nell’energia cinetica mentre la massa gravitazionale nell’energia potenziale. Se in un campo gravitazionale (dovuto a masse) sostituiamo all’energia potenziale l’energia cinetica:
1/2 mi v2 = GM*mg/r per la (1) si ricava v2 = 2GM/r (2)
La (2) indica la velocità che deve avere una particella, in un punto distante r da un corpo di massa M, affinché la sua energia cinetica sia eguale all’energia potenziale gravitazionale G*M/r in quel punto. Se sostituiamo la velocità v2 = 2GM/r nelle equazioni della Relatività Ristretta, si ricavano i valori del tempo e dello spazio deformati a causa della velocità v (posto c =1):
t’ = t /(1-v2) 1/2 = t /(1-2GM/r) 1/2 (3a) L’ = L*(1-2GM/r) 1/2 (3b) Vedi par. 3.2.: Relatività Generale (INFN)
Ossia nella relatività generale l’effetto del campo gravitazionale in un punto può essere sostituito da una deformazione dello spazio-tempo prodotto dalla massa M. Il fenomeno da dinamico diventa cinematico. Il corpo viene attratto verso uno spazio L’ più contratto? ed un tempo T’ più lento. Si può osservare che, tenuto conto della deformazione spazio-tempo, la velocità della luce (in caduta libera) rimane costante. Cioè è la contrazione dello spazio e la dilatazione del tempo a creare la sensazione dell’accelerazione mentre, in effetti, la velocità della luce rimane costante.
Come la luce rallenta e devia quando attraversa strati più densi di atmosfera, per effetto della  rifrazione, similmente, rallenta e devia quando passa vicino ad un corpo di grande massa. Il campo gravitazionale modifica quindi la densità dello spazio-tempo (l’indice di rifrazione del vuoto) .
rifrazione, similmente, rallenta e devia quando passa vicino ad un corpo di grande massa. Il campo gravitazionale modifica quindi la densità dello spazio-tempo (l’indice di rifrazione del vuoto) .